Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

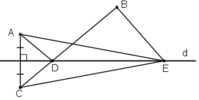
a) + A và C đối xứng qua d
⇒ d là trung trực của AC
⇒ AD = CD
⇒ AD + DB = CD + DB = CB (1)
+ E ∈ d ⇒ AE = CE
⇒ AE + EB = CE + EB (2)
+ CB < CE + EB (3)
Từ (1), (2), (3) ⇒ AD + DB < AE + EB
b) Vì với mọi E ∈ d thì AE + EB > AD + DB
Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.

Bài giải:
a) Ta có AD = CD
nên AD + DB = CD + DB = CB (1) 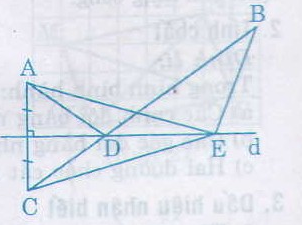
và AE = CE
nên AE + EB = CE + EB (2)
mà CB < CE + EB (3)
Nên từ (1) (2) và (3), suy ra
AD + DB < AE + EB
b) Theo câu a con đường ngắn nhất mà bạn Tú phải đi là con đường ADB

C đối xứng với A qua d => d là trung trực của AC
D; E thuộc d => EA = EC và DA = DC
ta có : AD + DB = DC + DB = CB
AE + EB = EC + EB
Trong tam giác BEC có: BC < EC + EB => AD + BD < AE + BE
b﴿ Giả sử bạn Tú đến điểm E bất kì trên d
ta có: Quãng đường bạn cần đi là AE + EB
mà AE + EB = CE + EB
ta luôn có: CE + EB ≥ CB
đê đi gần nhất thì CE + EB nhỏ nhất = CB
Dấu "=" xảy ra khi E trùng với D
vậy....

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC



Cách em làm đúng:)
Tuy nhiên nếu em học đường trung trực thì bài này có thể làm:
Ta có: A đối xứng với C qua đường thẳng d
=> d là đường trung trực của đoạn thẳng AC.
Do \(D\in d\Rightarrow DA=DC\)
Do \(E\in d\Rightarrow EA=EC\)
=> \(AD+DB=CD+BD=BC< BE+CE=BE+AE\)
=> Điều phải chứng minh.
Ngắn hơn đúng không :)
Nguyễn Linh Chi à đúng rồi! THầy em bảo dùng t/c đối xứng để làm:))