Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì A nằm trên đường trung trực của BC
nên AB=AC
Vì D nằm trên đường trung trực của BC
nen DB=DC
Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó:ΔABD=ΔACD
b: Gọi giao điểm của BC và AD là O
=>O là trung điểm của BC
Trường hợp 1: A,D nằm cùng phía
\(AO=\sqrt{AB^2-BO^2}=4.5\left(cm\right)\)
\(DO=\sqrt{6.5^2-6^2}=2.5\left(cm\right)\)
=>AD=2(cm)
TH2: A,D khác phía
\(AO=\sqrt{7.5^2-6^2}=4.5\left(cm\right)\)
\(DO=\sqrt{6.5^2-6^2}=2.5\left(cm\right)\)
AD=AO+DO=7(cm)

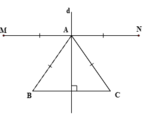
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN