Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(P\left(x\right)=x-2x^2+3x^5+x^4+x\)
\(\Leftrightarrow P\left(x\right)=\left(x+x\right)-2x^2+x^4+3x^5\)
\(\Leftrightarrow P\left(x\right)=2x-2x^2+x^4+3x^5\)
\(Q\left(x\right)=3-2x-2x^2+x^4-3x^5-x^4+4x^2\)
\(\Leftrightarrow Q\left(x\right)=3-2x+\left(-2x^2+4x^2\right)+\left(x^4-x^4\right)-3x^5\)
\(\Leftrightarrow Q\left(x\right)=3-2x+2x^2-3x^5\)
b)
\(P\left(x\right)+Q\left(x\right)=\left(2x-2x^2+3x^5+x^4\right)+\left(3-2x+2x^2-3x^5\right)\)
\(=2x-2x^2+3x^5+x^4+3-2x+2x^2-3x^5\)
\(=\left(2x-2x\right)+\left(3x^5-3x^5\right)+\left(-2x^2+2x^2\right)+x^4+3\)
\(=x^4+3\)
\(P\left(x\right)-Q\left(x\right)=\left(2x-2x^2+3x^5+x^4\right)-\left(3-2x+2x^2-3x^5\right)\)
\(=2x-2x^2+3x^5+x^4-3+2x-2x^2+3x^5\)
\(=\left(2x+2x\right)+\left(-2x^2-2x^2\right)+\left(3x^5+3x^5\right)+x^4-3\)
\(=4x-4x^2+6x^5+x^4-3\)
\(=6x^5+x^4-4x^2+4x-3\)

\(P\left(0\right)=3.0^4+0^3-0^2+\dfrac{1}{4}.0=0+0-0+0=0\)
\(Q\left(0\right)=0^4-4.0^3+0^2-4=0-0+0-4=-4\)
vậy Chứng tỏ x=0 là nghiệm của đa thức P(x), nhưng không phải là nghiệm của đa thức Q(x)

a) Ta có:
\(P\left(x\right)=x-2x^2+3x^5+x^4+x=3x^5+x^4-2x^2\)
\(Q\left(x\right)=3-2x-2x^2+x^4-3x^5-x^4+4x^2\)
\(=-3x^5+2x^2-2x+3\)
b) Ta có:
\(P\left(x\right)+Q\left(x\right)=3x^5+x^4-2x^2-3x^5+2x^2-2x+3\)
\(=x^4-2x+3\)
\(P\left(x\right)-Q\left(x\right)=3x^5+x^4-2x^2+3x^5-2x^2+2x-3\)
\(=6x^5+x^4-4x^2+2x-3\)
c) Ta có: \(P\left(0\right)=3.0^5+0^4-2.0^2=0\)
=> x = 0 là nghiệm của P(x)
Mà \(Q\left(0\right)=-3.0^5+2.0^2-2.0+3=3\)
=> x = 0 không là nghiệm của đa thức Q(x)

c: \(P\left(-1\right)=-3-5-4+2+6+4=0\)
Vậy: x=-1 là nghiệm của P(x)
\(Q\left(-1\right)=4+1+3+2-7+1=4< >0\)
=>x=-1 không là nghiệm của Q(x)

` P(x) = x^3-2x^2+x-2`
`Q(x) = 2x^3 - 4x^2+ 3x – 56`
a) `P(x) -Q(x)`
`= x^3-2x^2+x-2 - 2x^3 +4x^2 -3x +56`
`=(x^3-2x^3) +(4x^2-2x^2) +(x-3x) +(-2+56)`
`= -x^2 +2x^2 -2x +54`
b) Thay `x=2` vào `P(x)` ta đc
`P(2) = 2^3 -2*2^2 +2-2`
`= 8-8+2-2 =0`
Vậy chứng tỏ `x=2` là nghiệm của đa thức `P(x)`
Thay `x=2` vào `Q(x)` ta đc
`Q(2) = 2*2^3 -4*2^2 +3*2-56`
`=16 -16+6-56`
`= -50`
Vậy chứng tỏ `x=2` là ko nghiệm của đa thức `Q(x)`
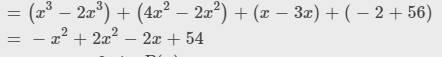
A(x)= 3x5+x4-2x2+2x
A(0)=3.05+04-2.02+2.0
=3.0+0-2.0+0
=0
Vậy x=0 là nghiệm của đa thức A(x)
B(x)= -3x5+2x2-2x+3
B(0)= -3.05+2.02-2.0+3
= -3.0+2.0-0+3
= 0+0+3
=3 khác 0
vậy x=0 không là nghiệm đa thức B(x)
xem nhé!