Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con lắc thứ hai có biên độ và tần số góc là: \(\left\{{}\begin{matrix}A_2=A_1=20cm\\\omega_2=\omega_1=20\pi\left(rad/s\right)\end{matrix}\right.\)
Chu kì của hai con lắc là: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20\pi}=0,1\left(s\right)\)
Hai con lắc lệch về thời gian so với con lắc thứ nhất một phần tư chu kì nên ta có:
\(\left[{}\begin{matrix}t_2=t_1+\dfrac{T}{4}\\t_2=t_1-\dfrac{T}{4}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x_2=20cos\left[20\pi\left(t+\dfrac{0,1}{4}\right)+\dfrac{\pi}{2}\right]\\x_2=20cos\left[20\pi\left(t-\dfrac{0,1}{4}\right)+\dfrac{\pi}{2}\right]\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x_2=20cos\left(20\pi t+\pi\right)\\x_2=20cos\left(20\pi t\right)\end{matrix}\right.\)

Cái kia lỗi công thức tí, mình làm lại đây nha=)
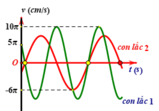
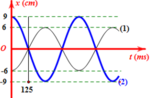
Phương trình vận tốc của vật trong dao động điều hòa là:
`[ v(t) = -A \omega \sin(\omega t + \varphi) ]`
Phương trình vận tốc của vật là:
`[ v(t) = -4\pi \sin(2\pi t + 0.5)) ]`
$HaNa$
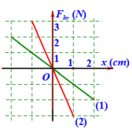
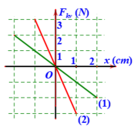


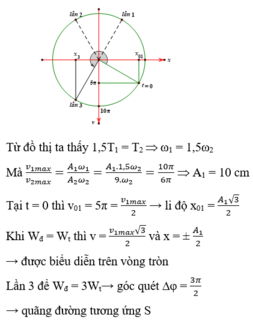


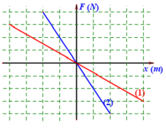
Quỹ đạo chuyển động của con lắc thứ nhất là:
\(A_2=4\cdot A_1=4\cdot5=20\left(cm\right)\)
Phương trình dao động của con lắc thứ 2 là: \(x=20\left(cos10\pi t+\dfrac{\pi}{6}+\dfrac{\pi}{2}\right)=20\left(cos10\pi t+\dfrac{2\pi}{3}\right)\left(cm\right)\)
phương trình dao động của con lắc thứ 2:
là 20(cos10πt + \(\dfrac{2\pi}{3}\)) cm