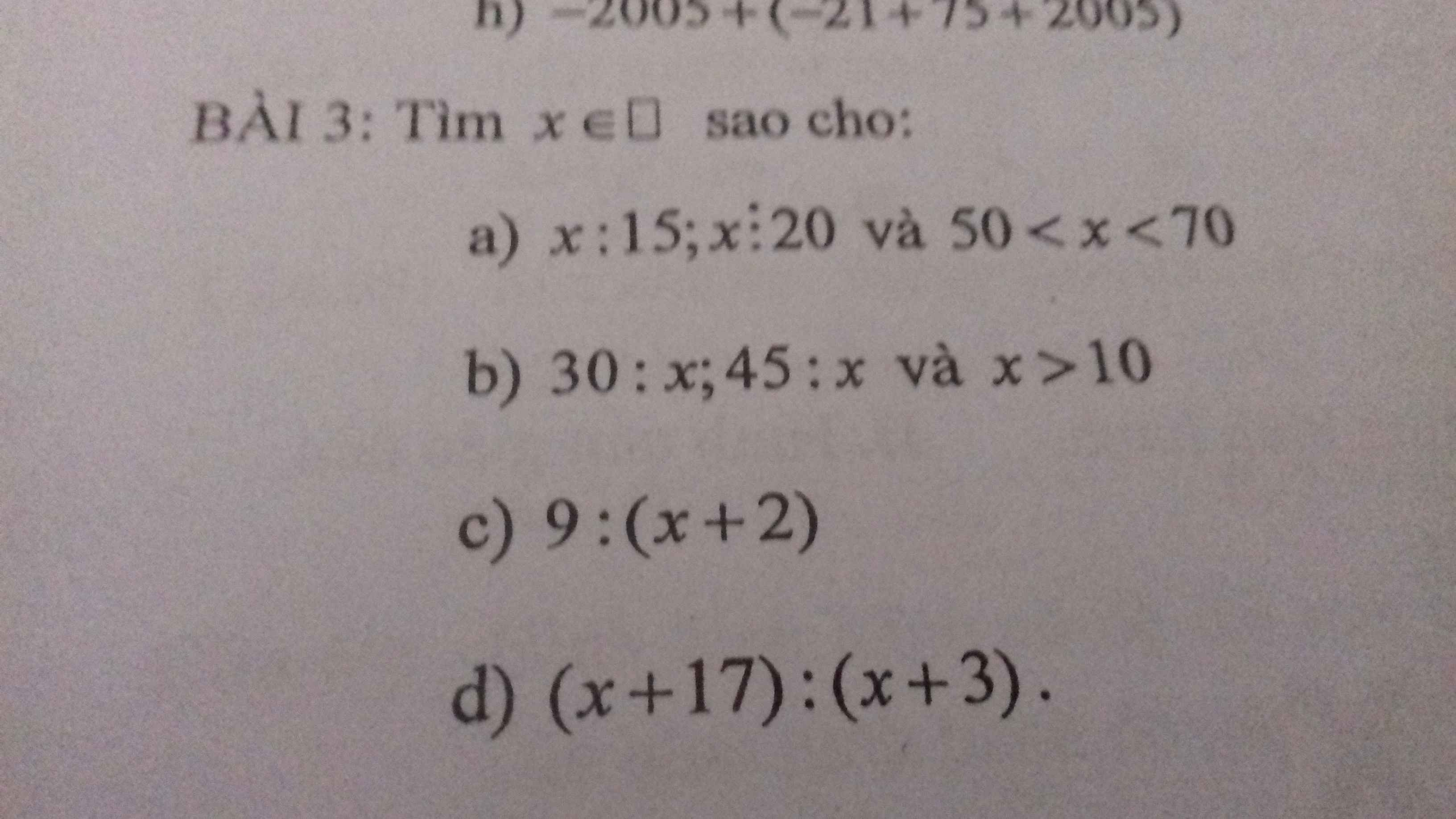Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* = { 1 ; 3; 9 }
Vậy có các số : 71 ; 73 ; 79
~ Học tốt ~

a) Ta thấy khoảng cách các số trong dãy là 2
=> Số hạng thứ 60 là:
2 + ( 60 - 1 ) * 2 = 122
b) Số hạng thứ 1005 của dãy là :
2 + ( 1005 - 1 ) * 2 = 2012
a,Số hạng thứ 60 là
2+(60-1).2=122
b,Số hạng thứ 1005 của dãy là
2+(1005-1).2=2012
hc tốt

bạn ghi sai đề kìa là xếp hàng 17,hàng 25 chứa ko phải là hàng 17, hàng 28
gọi số học sinh của trường đó là a ( a là số tụ nhiên khác 0)
ta có : a chia 17 dư 8; a chia 25 dư 16
\(\Rightarrow a+9⋮17\text{và} 25\)
\(\Rightarrow a+9\in BCNN\left(17,25\right)\)
mà BCNN(17,25)=425
\(a+9=425k \Rightarrow a=425k-9\)
mà 400<a<500 nên k=1
\(\Rightarrow425k-9=425.1-9=425-9=416\)(HS)
Vậy trong trường có 416 học sinh

=(1+4+42) +(43+44+45)+....+(42017+42018+42019)
=(1+4+42)+43(1+4+42)+.....+42017(1+4+42)
=(1+4+42)(1+43+46+....+42017)
=(1+4+16)(1+43+46+.....+42017)
=21(1+43+46+...+42017)
Vậy 21(1+43+46+.....+42017) chia hết cho 21
\(1+4+4^2+4^3+4^4+....+4^{2019}\)
\(=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+......+\left(4^{2017}+4^{2018}+4^{2019}\right)\)
\(=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+.....+4^{2017}\left(1+4+4^2\right)\)
\(=\left(1+4+4^2\right)\left(1+4^3+.....+4^{2017}\right)\)
\(=21\left(1+4^3+....+4^{2017}\right)\)
Mà \(21⋮21\Rightarrow21\left(1+4^3+.....+4^{2017}\right)⋮21\)
Vậy biểu thức trên chia hết cho 21(đpcm)

Vì số nguyên tố chẵn duy nhất là số 2 nên:
Nếu 3 số nguyên tố đó đều lớn hơn 2 thì tổng 3 số này phải là 1 số lẻ (tổng 3 số lẻ)
Mà 1012 là số chẵn nên trong 3 số có số 2.
Vậy số nhỏ nhất trong 3 số nguyên tố đó là số 2.

Ta có : \(12a+7b=64\)
Do \(64⋮4,12a⋮4\) \(\Rightarrow7b⋮4\) mà \(\left(7,4\right)=1\)
\(\Rightarrow b⋮4\) (1)
Từ giả thiết \(\Rightarrow7b\le64\) \(\Leftrightarrow b\le9\) kết hợp với (1)
\(\Rightarrow b\in\left\{4,8\right\}\)
+) Với \(b=4\) thì : \(12a+7\cdot4=64\)
\(\Leftrightarrow12a=36\)
\(\Leftrightarrow a=3\) ( thỏa mãn )
+) Với \(b=8\) thì \(12a+7\cdot8=64\)
\(\Leftrightarrow12a=8\)
\(\Leftrightarrow a=\frac{8}{12}\) ( loại )
Vậy : \(\left(a,b\right)=\left(3,4\right)\)

c: \(\Leftrightarrow x+2\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{-1;-3;1;-5;7;-11\right\}\)

\(P=2^{100}-2^{99}-2^{98}-...-2^3-2^2-2\)
\(\Rightarrow2P=2^{101}-2^{100}-...-2^2\)
\(\Rightarrow P=2P-P=2^{101}-2^{100}-...-2^2-2^{100}+2^{99}+2^{98}+...+2=2^{101}-2.2^{100}+2=2\)

b: \(\dfrac{x^2}{6}=\dfrac{24}{25}\)
nên \(x^2=\dfrac{144}{25}\)
=>x=12/5 hoặc x=-12/5
c: \(\left(x^4\right)^2=\dfrac{x^{12}}{x^5}\)
\(\Leftrightarrow x^8-x^7=0\)
hay \(x\in\left\{0;1\right\}\)
d: \(x^{12}=25x^{10}\)
\(\Leftrightarrow x^{10}\left(x^2-25\right)=0\)
hay \(x\in\left\{0;5;-5\right\}\)