

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải phương trình:
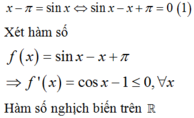
Phương trình (1) có tối đa 1 nghiệm. Mà f π = 0 ⇒ x = π là nghiệm duy nhất của (1).
Thể tích khối tròn xoay tạo thành là:
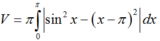
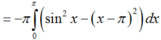
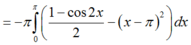

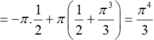
Mà
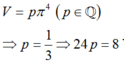
Chọn A.

Đáp án B
Ta có V = π ∫ 0 π − sin x 2 d x = π ∫ 0 π sin 2 x d x

Đáp án A.
Phương pháp:
Cho hai hàm số y = f x và y = g x liên tục trên a ; b . Khi đó thể tích vật thể tròn xoay giới hạn bởi hai đồ thị số y = f x , y = g x và hai đường thẳng x = a ; y = b khi quay quanh trục Ox là:
V = π ∫ a b f 2 x − g 2 x d x
Cách giải:
Phương trình hoành độ giao điểm: x 2 = 2 x ⇔ x = 0 x = 2
Thể tích cần tìm :
V = π ∫ 0 2 x 2 2 − 2 x 2 d x = π ∫ 0 2 x 4 − 4 x 2 d x = π ∫ 0 2 x 4 − 4 x 2 d x = π 1 5 x 5 − 4 3 x 3 2 0 .
= π 32 5 − 32 3 = 64 π 15

Phương trình hoành độ giao điểm: ![]()
• Thể tích vật thể khi quay phần S 1 quanh trục hoành là nửa khối cầu bán kính R = 2 nên có thể tích bằng
![]()
• Thể tích vật thể khi quay phần S 2 quanh trục hoành là
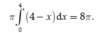
Vậy thể tích cần tính ![]()
Chọn A.

Chọn D.
Phương pháp: Chia miền cần tính thể tích làm 2 phần.
