Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

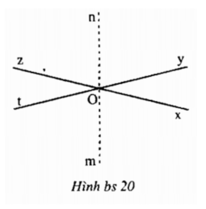
Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, hai góc zOy và tOx là hai góc đối đỉnh nên ∠zOy = ∠tOx.
Vì On, Om lần lượt là tia phân giác của góc zOy, góc xOt và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180° hay ∠mOn = 180º.
Suy ra Om và On là hai tia đối nhau.
Từ đó, hai góc ∠zOn và ∠mOx là hai góc đối đỉnh.

*Lời giải chi tiết:
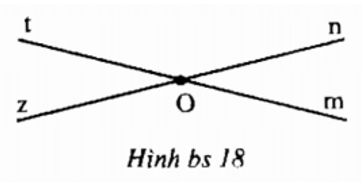
a) Vì góc nOt kề bù với góc mOn nên Ot là tia đối của tia Om. Tương tự, góc mOz kề bù với góc mOn nên Oz là hai tia đối của tia On. Từ đó, zOt và mOn là hai góc đối đỉnh.
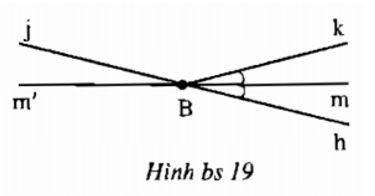
b) Vì góc kBj kề bù với góc hBk nên Bj là tia đối của tia Bh. Từ đó, m’Bj và hBm là hai góc đối đỉnh.
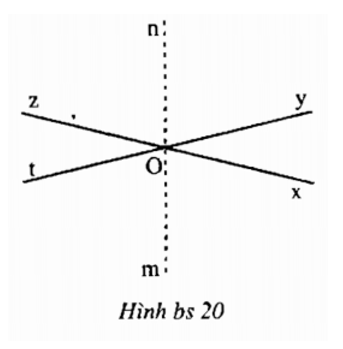
c) Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, zOy và tOx là hai góc đối đỉnh, tức là ∠zOy = ∠tOx.
Vì On, Om đều là tia phân giác và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180°.
Suy ra Om và On là hai tia đối nhau.
Từ đó, ∠zOn và ∠mOx là hai góc đối đỉnh.

Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1)
Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng
\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh
⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)
Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 1800 (gt)
⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) = 1800
⇒ Om và On cùng thuộc một đường thẳng mn (2)
Kết hợp (1) và (2) ta có: góc zOn và góc xOm là hai góc đối đỉnh

Bài làm :
Bạn tự vẽ hình nhé
Om là phân giác góc xOy
\(\Rightarrow\widehat{xOm}=\frac{\widehat{xOy}}{2}=\frac{120}{2}=60^o\left(1\right)\)
Góc yOz kề bù góc xOy
\(\Rightarrow\widehat{xOz}=\widehat{yOz}-\widehat{yOx}=180-120=60^o\)
On là phân giác góc yOz
\(\Rightarrow\widehat{xOn}=\frac{\widehat{xOz}}{2}=\frac{60}{2}=30^o\left(2\right)\)
Cộng (1) với (2)
\(\Rightarrow\widehat{xOm}+\widehat{xOn}=60+30\)
\(\Leftrightarrow\widehat{mOn}=90^o\)
\(\Rightarrow Om\perp On\)
=> Điều phải chứng minh
Vì Om là tia phân giác góc xOy
=> \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}=\frac{1}{2}.120^0\)\(=60^0\)
Vì góc xOy kề bù góc yOz nên góc yOz = 180 độ - 120 độ = 60 độ
Vì On là tia phân giác góc yOz
=> \(\widehat{yOn}=\widehat{nOz}=\frac{1}{2}.\widehat{yOz}=\frac{60^0}{2}=30^0\)
=> \(\widehat{mOy}+\widehat{yOn}=60^0+30^0=90^0\)
=> \(\widehat{mOn}=90^0\)
=> Om vuông góc với On
Bài này có thể viết thành dạng tổng quát được nhé bạn!
Om là tia phân giác góc xOy, On là tia phân giác yOz mà góc xOy và yOz kề bù
=> Om vuông On

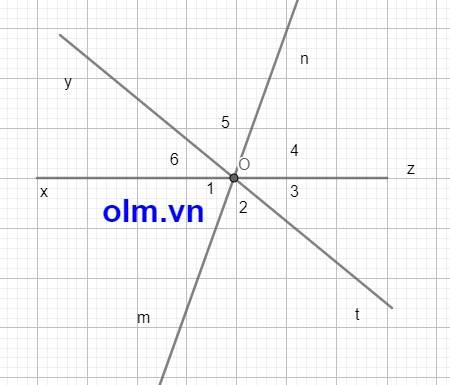
bạn chứng minh mOn là góc bẹt =>Om và On đối nhau
và oz õ cũng Cm tuuwong tự
thì hai góc đấy đối đỉnh