Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
chung
Do đó: ΔOAM=ΔOBN
=> và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>
=>OK là phân giác của
Xin lỗi bạn, hồi nãy câu trả lời của mình bị lỗi. Giờ mình xin phép sửa lại chút nha:


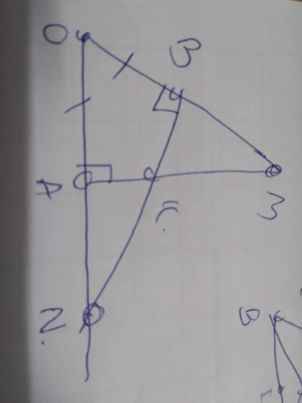

a/ Xét ΔOAE và ΔOBF có:
+) OA = OB (GT)
+) O: góc chung.
+) ∠A = ∠B = 90o (gt)
⇒ ΔOAE = ΔOBF ( g.c.g )
⇒ AE = BF ( 2 góc tương ứng )
---
b/ Có:
+) ∠E = ∠F ( vì ΔOAE = Δ OBF ) (1)
+) ∠OAI = ∠OBI ( gt )
Mà: ∠OAI + ∠IAF = ∠OBI + ∠IBE = 180o( kề bù )
⇒ ∠IAF = ∠IBE. (2)
⇔ AF = BE. (3)
Từ (1), (2) và (3) ⇒ ΔAFI = ΔBEI ( g.c.g )
---
c/ Xét ΔAIO và ΔBIO có:
+) OA = OB ( gt )
+) I: cạnh chung.
+) AI = BI ( vì ΔAFI = ΔBEI )
⇒ ΔAIO = ΔBIO ( c.c.c )
⇒ ∠AOI = ∠BOI ( 2 cạnh tương ứng )
⇒ OI là phân giác của ∠AOB. ( đpcm )
~ Chúc bn hc tốt!^^ ~

a, xét tam giác AOE và tam giác BOF có :
OA = OB (gt)
\(\widehat{A}=\widehat{B}=90^0\)
\(\widehat{O}\)là góc chung
suy ra : tam giác AOE = tam giác BOF
suy ra : AE = BF ( cạnh tương ứng )
Hình tự vẽ nha
a)Xét tam giác AEO vuông tại A và tam giác BFO vuông tại B có :
-\(\widehat{O}\)là góc chung
-OA=OB ( GT )
=> Tam giác AEO = Tam giác BFO ( cạnh góc vuông và góc nhọn kề )
=>AE=BF ( tương ứng )
b)Vì tam giác AEO = tam giác BFO ( CM trên )
=>OF=OE ( tương ứng )
\(\widehat{ÒFB}=\widehat{OEA}\)( tương ứng )
Ta có : OB+BE=OE
OA+AF=OF
mà OF=OE ; OA=OA
=>AF=BE
Xét tam giác AFI vuông tại A và tam giác BEI vuông tại B ta có :
BE=AF ( CM trên )
\(\widehat{ÒFB}=\widehat{OEA}\)( CM trên )
=> Tam giác AFI = tam giác BEI ( cạnh góc vuông và góc nhọn kề )
c) Vì tam giác AFI = tam giác BEI ( CM trên )
=>BI=AI ( tương ứng )
Xét tam giác AOI và tam giác BOI có
OA=OB (GT)
OI là cạnh chung
BI=AI ( CM trên )
=> tam giác AOI = tam giác BOI (c.c.c)
=>\(\widehat{AOI}=\widehat{BOI}\)( tương ứng )
=> OI là tia phân giác của \(\widehat{AOB}\)

a) Xét ΔAOC vuông tại A và ΔOBD vuông tại B có
OA=OB(gt)
∠Olà góc chung
⇒ΔAOC=ΔOBD(cạnh góc vuông-góc nhọn kề)
b) Xét ΔOIB vuông tại B và ΔOIA vuông tại A có
OI là cạnh chung
OB=OA(gt)
⇒ ΔOIB=ΔOIA(cạnh huyền-cạnh góc vuông)
⇒IB=IA(hai cạnh tương ứng)
Ta có: IB+ID=BD(do B,I,D thẳng hàng)
IA+IC=AC(do A,I,C thẳng hàng)
MàIB=IA(cmt)
và BD=AC(do ΔAOC=ΔOBD)
⇒ ID=IC
Xét ΔIDC có ID=IC(cmt)
⇒ ΔIDC cân tại I
c) Ta có: ΔOIB=ΔOIA(cmt)
⇒∠BIO=∠AIO(hai góc tương ứng)
Mà tia IO nằm giữa hai tia IA,IB
⇒IO là tia phân giác của∠AIB

mik biet moi i a) và b) thui
a) xét tam giác AOM và tam giác BOM ta có :
OA = OB ( GIẢ THIẾT )
góc AOM = góc MOB
OM là cạnh chung
=> tam giác AOM = tam giác BOM
b) từ a) => am = bm

Ta có hình vẽ:
x O y A B E F I a/ Xét tam giác OAE và tam giác OBF có:
OA = OB (GT)
O: góc chung
\(\widehat{A}\)=\(\widehat{B}\)=900 (GT)
=> tam giác OAE = tam giác OBF (g.c.g)
=> AE = BF (2 góc tương ứng)
b/ Ta có: \(\widehat{E}\)=\(\widehat{F}\) (vì tam giác OAE = tam giác OBF)(1)
Ta có: \(\widehat{OAI}\)=\(\widehat{OBI}\)(GT) (*)
Mà \(\widehat{OAI}\)+\(\widehat{IAF}\)=1800 (kề bù) (**)
và \(\widehat{OBI}\)+\(\widehat{IBE}\)=1800 (kề bù) (***)
Từ (*),(**),(***) => \(\widehat{IAF}\)=\(\widehat{IBE}\) (2)
Ta có: AF = BE (3)
Từ (1),(2),(3) => tam giác AFI = tam giác BEI (g.c.g)
c/ Xét tam giác AIO và tam giác BIO có:
OI: cạnh chung
OA = OB (GT)
AI = BI (vì tam giác AFI = tam giác BEI)
=> tam giác AIO = tam giác BIO (c.c.c)
=> \(\widehat{AOI}\)=\(\widehat{BOI}\) (2 góc tương ứng)
=> OI là phân giác \(\widehat{AOB}\) (đpcm)
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOB}\) chung
Do đó: ΔOAM=ΔOBN
=>\(\widehat{OMA}=\widehat{ONB}\) và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
\(\widehat{KNA}=\widehat{KMB}\)
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>\(\widehat{AOK}=\widehat{BOK}\)
=>OK là phân giác của \(\widehat{AOB}\)
bạn vẽ hình hộ mình với ạ!!!!