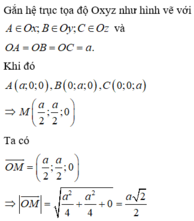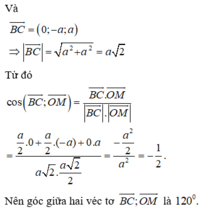Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{yOz}=180^0-120^0=60^0\)
b: \(\widehat{aOb}=\dfrac{180^0}{2}=90^0\)

b,
do OA=OC, OB=OC=> AB=CD
mặt khác, xét 2 tam giác BCO và tam giác ADO
BC=AD (từ câu a)
BO=DO
CO=AO
=`> tg OBC=ODA (c.c.c) => góc OBC= góc ODA (hai góc tương ứng
xét hai tam IBA và ICD
AB=CD
góc IBA=IDC
góc BIA=DIC(hai góc đối dỉnh)
=> tg IBA=IDC(g.c.g) => IB=ID, IC=IA (các cạp cạnh tương ứng)
c,
ta đã có tg OBC= tg ODA => góc BCO = góc DAO
xét hai tg AIO và CIO
OA=OC (gt)
IA=IC
góc BCO = góc DAO
=> tg AIO= tg CIO (c.g.c) => góc IOC = góc IOA (hai góc tương ứng ) => Oi là tia phân giác của AOC hay góc xOy

Xét tam giác OBC và tam giác ODA có
góc O chung
OA=OA(gt)
OB=OD(gt)
=> Tam giác OBC=ODA(c-g-c)
=> BC=AD(cạnh tương ứng)

Đáp án A
Gọi I là hình chiếu của O trên BC, H là hình chiếu của O trên AI.
Suy ra d = OH.
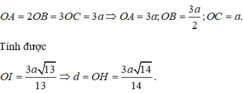

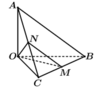
Đặt
O
A
=
O
B
=
O
C
= a suy ra ![]()
Gọi N là trung điểm AC, ta có MN//AB. Khi đó ![]()
Trong tam giác OMN có ![]() nên OMN là tam giác đều
nên OMN là tam giác đều
![]()
Chọn C.

Mình ko vẽ hình vào máy được nên giải trước nhé!!!
Vì OC là tia phân giác của góc AOB=> góc AOC = góc COB= 1/2 góc AOB=140*:2=70*
Vì tia OD là tia đối của tia OA=> góc AOD là góc bẹt=> góc AOD=180*
=>Tia OC nằm giũa tia OD và OA
=> AÔC+ CÔD = AÔD
Thay số: 70*+ CÔD = 180*
=> CÔD= 180*-70*=110*
Vậy góc COD=110*