
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



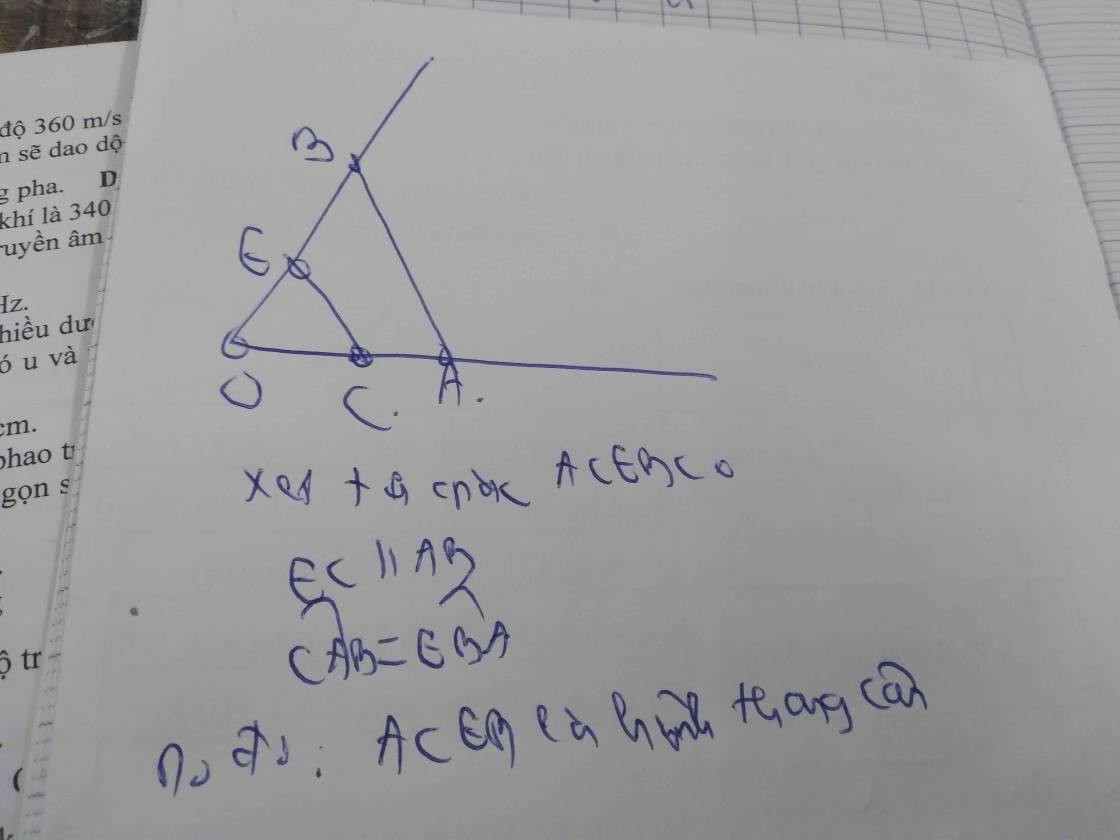
Xét tứgiác ACEB có
EC//AB
góc CAB=góc EBA
Do đó: ACEB là hình thang cân

A O B x y 1 1 C E
Tg ABEC có CE // AB ( gt )
=> Tg ABEC là hình thang
+) ΔOAB có OA = OB ( gt )
=> ΔOAB cân ở O
=> \(\widehat{A_1}=\widehat{B_1}\)
+) Hình thang ABEC có \(\widehat{A_1}=\widehat{B_1}\)
=> Hình thang ABEC là hình thang cân ( DHNB hình thang cân )

a: Xét ΔOAH và ΔOBH có
AO=BO
OH chung
AH=BH
=>ΔOHA=ΔOHB
b: ΔOHA=ΔOHB
=>góc OHA=góc OHB=180/2=90 độ
=>OH vuông góc AB
c: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC

Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.
Áp dụng định lí Thalès vào tam giác OBD, ta có:
\(\dfrac{{OA}}{{OB}} = \dfrac{{OC}}{{O{\rm{D}}}}\) hay \(\dfrac{2}{5} = \dfrac{3}{{O{\rm{D}}}}\)
Suy ra: \(O{\rm{D}} = \dfrac{{5.3}}{2} = 7,5(cm)\)
Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).
Vậy CD = 4,5 cm.