Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì \(\left\{{}\begin{matrix}OA=OC\\OB=OD\\\widehat{DOB}.chung\end{matrix}\right.\) nên \(\Delta OAD=\Delta OCB\left(c.g.c\right)\)

Sửa `a)` CM tam giác OAD=tam giác OCB
`a)`
Xét `Delta OAD` và `Delta OCB` có :
`{:(OD=OB(GT)),(hat(O)-chung),(OA=OC(GT)):}}`
`=>Delta OAD=Delta OCB(c.g.c)(đpcm)`
`b)`
`Delta OAD=Delta OCB(cmt)=>hat(D_1)=hat(B_1)` ( 2 góc t/ứng )
Có `OC=OA;OB=OD(GT)`
`=>OB-OA=OD-OC`
hay `AB=CD`
Có `OC=OA(GT)`
`=>Delta OAC` cân tại `O`
`=>hat(C_1)=hat(A_1)`
mà `hat(C_1)+hat(ACD)=180^0` ( kề bù )
`hat(A_1)+hat(CAB)=180^0` ( kề bù )
nên `hat(ACD)=hat(CAB)`
Xét `Delta ACD` và `Delta CAB` có :
`{:(hat(D_1)=hat(B_1)(cmt)),(CD=AB(cmt)),(hat(ACD)=hat(CAB)(cmt)):}}`
`=>Delta ACD=Delta CAB(c.g.c)(đpcm)`
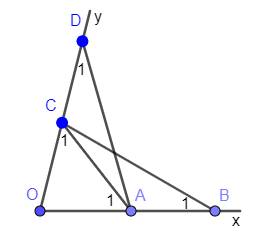

Hình tự vẽ nhé
Xét △OAD và △OCB, có
OA=OC (giả thiết)
Góc AOD chung
OD=OB(giả thiết)
=> △OAD=△OCB (cgc)
b) vì △OAD=△OCB
=> AD=BC
lại có: AB = OB-OA
CD = OD-OC
=> AB=CD
Xét △CAB và △ACD, có
AC cạnh chung
AB=CD
AD=CB
=> △CAB=△ACD
cho tam giác ABC có góc A=80 độ.dựng AH vuông góc với BC(H thuộc BC).Trên ttia đối của tia HA lấy điểm D sao cho HD=HA. câu a, chứng minh AC=DC câu b, chứng minh tam giác ABC= tam giác DBC câu c, TÍNH SỐ ĐO GÓC bdc

Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OCB có
-O : góc chung
-OA = OC
-OB = OD
=> tam giác OAD = tam giác OCB
b/ Xét tam giác ACD và tam giác CAB có
-AC: cạnh chung
-OA = OC
OB = OD
\(\Rightarrow\)AB = CD
-AD = CB (vì \(\Delta\)OAD=\(\Delta\)OCB)
Vậy tam giác ACD = tam giác CAB

a: Xét ΔOAD và ΔOCB có
OA=OC
ˆOO^ chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

