Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y'yBDACMFE
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE.

Xét ΔODB và ΔOCA có
\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\left(\dfrac{3}{6}=\dfrac{4}{8}\right)\)
\(\widehat{O}\) chung
Do đó: ΔODB đồng dạng với ΔOCA
=>\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\)
=>\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
Xét ΔODC và ΔOBA có
\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
\(\widehat{O}\) chung
Do đó: ΔODC đồng dạng với ΔOBA
=>\(\dfrac{DC}{BA}=\dfrac{OC}{OA}\)
=>\(\dfrac{DC}{5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(DC=3\cdot\dfrac{5}{4}=\dfrac{15}{4}=3,75\left(cm\right)\)

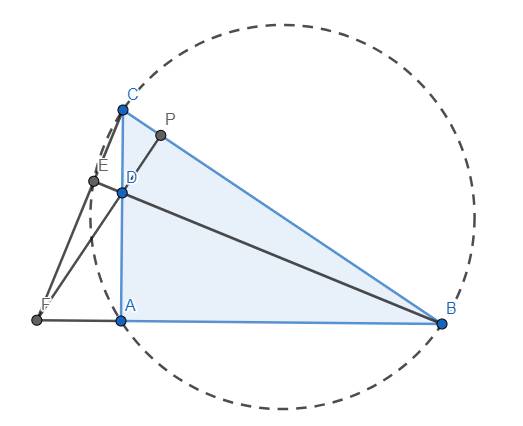
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.
(Tự vẽ hình)
Không mất tính tổng quát giả sử điểm A nằm giữa hai điểm O, B và điểm D nằm giữa hai điểm O,C.
Theo bài ra ta có: \(OA.OB=OC.OD\Leftrightarrow\frac{OA}{OC}=\frac{OD}{OB}\)
Kết hợp với \(\widehat{AOD}=\widehat{COB}\) (hai góc trùng nhau), ta được \(\Delta OAD\) \(\sim\)\(\Delta OCB\) (c.g.c).
Suy ra \(\widehat{ADO}=\widehat{CBO}\), do đó ABCD là tứ giác nội tiếp.
Vậy A, B, C, D cùng thuộc một đường tròn