Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 :
A B O C x z y
Xét tam giác OAB và tam giác OAC có :
góc AOB = góc AOC (gt)
góc OBA = góc OCA ( =90 độ )
OA chung
=> tam giác OAB = tam giác OAC ( cạnh huyền - góc nhọn )
=> AB=AC (đpcm)
*) Nhận xét : Tập hợp các điểm nằm trên tia phân giác của 1 góc thì cách đều hai tia tạo nên góc đó.

a) Vì Ay' // Oy
=> y'AO + AOy' = 180° ( trong cùng phía)
=> y'AO = 30°
Vì Ay' // Oy
=> xAy' = AOy = 30° ( đồng vị)
b) Vì At' là phân giác xAy'
=> xAt' = t'Ay' = 30°/2 = 15°
Vì Ot là phân giác AOy
=> AOt = yOt = 30/2 = 15°
=> xAt' = AOt = 15°
Mà 2 góc này ở vị trí đồng vị
=> At' // Ot

Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.

Ta có: góc xOy = 1500 x z a z o y 150o
Mà góc OAz = 300
=> góc xOy + góc OAz = 1800
Mà hai góc này ở vị trí TCP
=> Az // Oy
Vì Az' là tia đối của Az
Nên zz' // Oy (đpcm).
OM là phân giác của ˆxOyxOy^
⇒ˆxOM=ˆyOM=ˆxOy2=70o⇒xOM^=yOM^=xOy^2=70o
Ta có zz,//Oy
⇒ˆOAz,=ˆAOy⇒OAz,^=AOy^ mà ˆAOy=150o⇒ˆOAz,=150oAOy^=150o⇒OAz,^=150o
AN là phân giác của ˆOAz,OAz,^
⇒ˆNAz,=ˆNAO=ˆOAz,2=70o⇒NAz,^=NAO^=OAz,^2=70o
Ta có ˆNAO=ˆAOM=70oNAO^=AOM^=70o mà chúng ở vị trí so le trong do AO cắt AN và OM
=> AN//OM
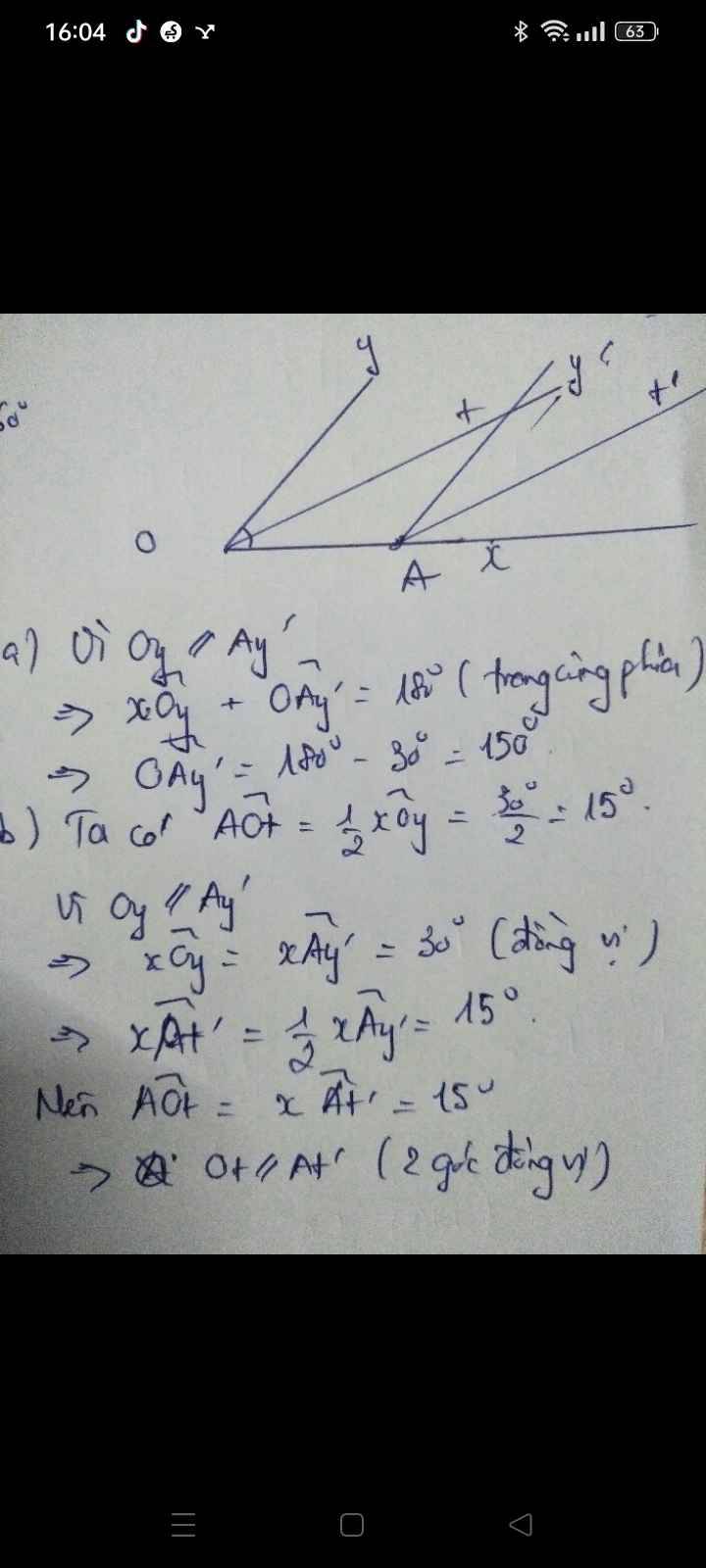
x O y A B C
Ta nối O với A.
Xét \(\Delta OAB\) và \(\Delta OAC\) có :
\(\hept{\begin{cases}\widehat{OBA}=\widehat{OCA=90^o}\\OAchung\\OB=OC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta OAB=\Delta OAC\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BOA}=\widehat{COA}\)
\(\Rightarrow OA\) là tia phân giác của \(\widehat{xOy}\)
*) Nhận xét : Tập hợp các điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.