Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tia Ot là tia phân giác của xOy, ta có:
xOt = tOy = xOy / 2 = 500 / 2 = 250
Vì góc tOy và yOm kề nhau, nên:
tOy + yOm = tOm
hay 250 + yOm = 900
=> yOm = 900 - 250
=> yOm = 650
b) Vì góc xOy và yOz là 2 góc kề bù, nên ta có:
xOy + yOz = 1800
Hay 500 + yOz = 1800
=> yOz = 1800 - 500
=> yOz = 1300
Vì 1300> 650 nên suy ra tia Om ko phải là tia phân giác của góc yOz
Ps : Ko chắc, lâu wá wên oy! :v
:( Học tốt!

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(60^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
b) Ta có: tia Ot nằm giữa hai tia Ox và Oy(cmt)
nên \(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOt}+60^0=120^0\)
hay \(\widehat{yOt}=60^0\)
Ta có: \(\widehat{xOt}=60^0\)(gt)
mà \(\widehat{yOt}=60^0\)(cmt)
nên \(\widehat{xOt}=\widehat{yOt}\)
c) Ta có: tia Ot nằm giữa hai tia Ox và Oy(cmt)
mà \(\widehat{xOt}=\widehat{yOt}\)(cmt)
nên Ot là tia phân giác của \(\widehat{xOy}\)
d) Ta có: Om là tia phân giác của \(\widehat{xOt}\)
nên \(\widehat{xOm}=\dfrac{60^0}{2}=30^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOm}< \widehat{xOy}\left(30^0< 120^0\right)\)
nên tia Om nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOm}+\widehat{mOy}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{mOy}+30^0=120^0\)
hay \(\widehat{mOy}=90^0\)

a/ vì xoy > xot
=> ot là tia nằm giữa hai tia ox ,oy
b/ vì ot nằm giữa nên ta có hệ thức yot + tox = xoy
=> toy = xoy - tox
= 60 - 30 = 30 độ
=> toy = xot
c/ ot là tia pân giác xoy
vì yot + tox = xoy
yot = tox = 30 độ
d/ vì om là tia phân giác xot
=> tom = mox = tox : 2
= 30 : 2 = 15 độ
vì mot < toy
=> ot là tia nằm giữa hai tia om, oy
vậy moy = yot + tom
= 30 + 15 = 45 độ

a, trên nửa mặt phẳng bờ chứa tia Ox có \(\widehat{xOt}\)= 40 độ, \(\widehat{xOy}\)=80 độ
Vì 40 độ<80 độ nên \(\widehat{xOt}\)<\(\widehat{xoy}\)
\(\Rightarrow\)tia Ot nằm giữa 2 tia Ox và Oy (1)
b,Vì tia Ot nằm giữa hai tia Ox và Oy
\(\Rightarrow\)\(\widehat{xOt}\)+\(\widehat{tOy}\)=\(\widehat{xOy}\)
40 độ +\(\widehat{tOy}\)=80 độ
\(\Rightarrow\)\(\widehat{tOy}\)=80 độ-40 độ
\(\Rightarrow\)\(\widehat{tOy}\)=40 độ
Ta thấy:
\(\widehat{tOy}\)=40 độ
\(\widehat{xOy=80}độ\)
40 độ< 80độ
\(\Rightarrow\)\(\widehat{tOy< xOy}\)
Ta thấy:
\(\widehat{xOt=40}độ\)
\(\widehat{tOy=40}độ\)\(\Rightarrow\)\(\widehat{xOt=tOy}\)(2)
40 độ=40 độ
Từ (1) và (2)
\(\Rightarrow\)Tia Ot là tia phân giác của \(\widehat{xOy}\)
d,Vì Ox và Oz là 2 tia đối nhau
\(\Rightarrow\)\(\widehat{zOy}\)và \(\widehat{xOy}\) là 2 góc kề bù
\(\Rightarrow\)\(\widehat{zOy+xOy=180độ}\)
\(\Rightarrow\)\(\widehat{zOy+80độ=180độ}\)
\(\Rightarrow\)\(\widehat{zOy=180độ-80độ}\)
\(\Rightarrow\)\(\widehat{zOy=100độ}\)
trên nửa mặt phẳng bờ cứa tia Oz có \(\widehat{zOm}\)=50độ,\(\widehat{zOy}\)=100độ
vì 50 độ <100 độ nên \(\widehat{zOm< zOy}\)
\(\Rightarrow\)tia Om nằm giữa 2 tia Oz và Oy
\(\Rightarrow\)\(\widehat{zOm+mOy=zOy}\)
\(\Rightarrow\)50 độ +\(\widehat{mOy}\)=100 độ
\(\Rightarrow\)\(\widehat{mOy}\)= 100 độ -50 độ
\(\Rightarrow\)\(\widehat{mOy=50}độ\)
a) trên cùng một nữa mặt phẳng có: xOt < xOy
=> Ot nằm giữa 2 tia Ox,Oy
b) vì Ot nằm giữa 2 tia Ox ,Oy:
ta có: xOt + tOy = xOy
=> tOy = xOy - xOt (1)
thay: xOy=80' ; xOt=40' vào (1)
ta có: tOy = 80 - 40
=> tOy = 40' (2)
ta có: xOt = 40' (3)
từ (2) và (3) :
=> xOt = tOy
c) trên cùng 1 nửa mặt thẳng

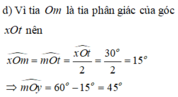
Vì tia ot và om k nằm ở 1 điểm nhất định nên
=> Các trường hợp
TH1 : \(\widehat{xOy}=\widehat{tOy}\) và \(\widehat{tOy}=\widehat{yOm}\)
=> Oy và Om là tia phân của các góc
\(\Rightarrow\widehat{xOt}=\widehat{yOm}\)
TH2 : \(\widehat{xOt}>\widehat{tOy}\) và \(\widehat{tOy}>\widehat{yOm}\)
+ Nếu \(\widehat{xOt}\) bé hơn \(\widehat{yOm}\) ( về đơn vị ) thì \(\widehat{xOt}< \widehat{yOm}\)
+ Nếu \(\widehat{xOt}\) lớn hơn \(\widehat{yOm}\) ( về đơn vị ) thì \(\widehat{xOt}>\widehat{yOm}\)
+ Nếu \(\widehat{yOm}\) bằng \(\widehat{xOt}\) ( trùng khớp ) thì \(\widehat{yOm}=\widehat{xOt}\)
TH3 : \(\widehat{xOt}>\widehat{tOy}\) và \(\widehat{tOy}< \widehat{yOm}\)
\(\Rightarrow\widehat{xOt}=\widehat{yOm}\) và lớn hơn \(\widehat{tOy}\) . Nên \(\widehat{xOt}=\widehat{yOm}\)