Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)

O y z x B A I M D C / /
a) Vì tia Oz là tia phân giác \(\widehat{xOy}\) :
=> \(\widehat{xOz}=\widehat{zOy}=\dfrac{\widehat{xOy}}{2}=\dfrac{60^0}{2}=30^0\)
=> \(\widehat{zOy}=30^0\)
b) Xét \(\Delta OIAvà\Delta OIBcó:\)
OI (chung)
\(\widehat{AOI}=\widehat{BOI}\) (OI là tia phân giác \(\widehat{xOy}\) )
OA = OB ( gt)
Do đó: \(\Delta OIA=\Delta OIB\left(c-g-c\right)\)
c) Vì \(\Delta OIA=\Delta OIB\left(cmt\right)\)
=> \(\widehat{BIO}=\widehat{AIO}\) (hai góc tương ứng)
mà \(\widehat{BIO}+\widehat{AIO}=180^0\) (kề bù)
=> \(\widehat{BIO}=\widehat{AIO}=90^0\)
=> \(OI\perp AB\)
d) Xét \(\Delta BOMvà\Delta AOMcó:\)
OM (chung)
\(\widehat{BOM}=\widehat{AOM}\) (OM là tia phân giác \(\widehat{xOy}\) )
OB = OA (gt)
Do đó: \(\Delta BOM=\Delta AOM\left(c-g-c\right)\)
=> MA = MB (hai cạnh tương ứng)
e) Vì OI \(\perp\) AB
mà AB // DC
=> \(OI\perp DC\)
mà I và M cùng nằm trên tia Oz
=> \(OM\perp DC\)
=> \(\widehat{DMO}=\widehat{CMO}=90^0\)
Xét \(\Delta DOMvà\Delta COMcó:\)
OM (chung)
\(\widehat{DOM}=\widehat{COM}\) (OM là tia phân giác \(\widehat{xOy}\) )
\(\widehat{DMO}=\widehat{CMO}\left(cmt\right)\)
Do đó: \(\Delta DOM=\Delta COM\left(g-c-g\right)\)
=> OD = OC (hai cạnh tương ứng)
mà OB = OA
BD = OD - OB
AC = OC - OA
=> BD = AC (đpcm)

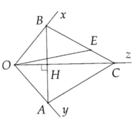
a) xet tam giac OAH va tam giac OBH : OH=OH ( canh chung ), OA=OB (gt), goc HOA= goc HOB( Ot la tia p/g goc xOy)-> tam giac = nhau (c-g-c)
b) cm tam giac OHB= tam giac AHC (c=g=c) ; OH=HC , BH=AH (tam giac OAH=tam giac OBH), goc OHB= goc CHA( 2 goc doi dinh)
c) C1 : cm tam giac OAB can tai O co OH la phan giac -> OH la duong cao -> OH vuong goc AB hay OC vuong goc AB
C2 : ta co : goc OHB+ goc OHA=180 ( 2 goc ke bu)
goc OHB= goc OHA( tam giac OHA= tam giac OHB )
--> goc OHB+goc OHB=180
-> 2 gpc OHB=180
->goc OHB=180:2=90
-> OH vuong goc AH tai H hay OC vuong goc AB

nhầm nhầm tôi cần câu e
cíu tui please
Xét tam giác OBM và tam giác OAM có:
OA=OB; góc BOM=góc AOM; OM chung
=> Tam giác OBM= tam giác OAM
=> MA=MB