Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

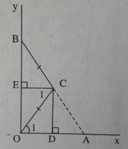
+) Vì CE // OD (cùng vuông góc với OB) ⇒ ∠C1 = ∠O1 (so le trong)
+) Xét ΔOCE và ΔCOD có:
OC chung
∠C1 = ∠O1 ( chứng minh trên )
∠OEC = ∠ODC = 90º
Suy ra: ΔOCE = ΔCOD (cạnh huyền – góc nhọn) ⇒ CE = OD.

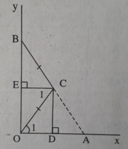
CD // OE (cùng vuông góc OA) ⇒ ∠(BEC) = ∠(ECD) (so le trong)
Ta lại có ∠(BEC) = 90o nên ∠(ECD) = 90o.
Vậy CE ⊥ CD.

a: Xét tứ giác ODCE có
OD//CE
OE//CD
Do đó: ODCE là hình bình hành
Suy ra: CE=OD
b: Hình bình hành ODCE có \(\widehat{EOD}=90^0\)
nên ODCE là hình chữ nhật
Suy ra: CE\(\perp\)CD
d: Xét tứ giác CEDA có
CE//DA
CE=DA
Do đó: CEDA là hình bình hành
Suy ra: CA//DE

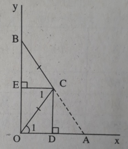
CD là đường trung trực của OA ⇒ CO = CA (tính chất đường trung trực) (1) .
CE là đường trung trực của OB ⇒ CO = CB (tính chất đường trung trực) (2).
Từ (1) và (2) suy ra: CA = CB.

(h.114) Ta có CE = OD (câu a))
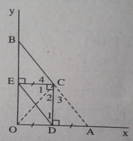
mà OD = DA (do D là trung điểm OA) nên CE = DA.
Xét ΔECD và ΔADC có:
CD chung
CE = DA( chứng minh trên)
∠(ECD) = ∠(CDA) = 90º
Do đó ΔECD = ΔADC (c.g.c)
⇒ ∠D1 = ∠C3 ⇒ CA // DE (hai góc so le trong bằng nhau).

c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).