Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

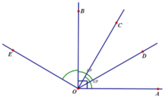
Hình tự vẽ nha bạn
Ta có: ∠ AOC + ∠ BOC = ∠ AOB
⇒ 60o + ∠ BOC = 90o
⇒ ∠ BOC = 30o (1)
Lại có: ∠ BOC + ∠ COD = ∠ BOD
⇒ 30o + ∠COD = 60o
⇒ ∠ COD = 30o (2)
Từ (1) và (2) ⇒ ∠ BOC = ∠ COD = 30o
Suy ra: OC là phân giác của ∠ BOD
Ta có: ∠ COD + ∠ AOD = ∠ AOC
⇒ 30o + ∠ AOD = 60o
⇒ ∠ AOD = 30o
Vì ∠ COD = ∠ AOD = 30o nên OD là phân giác của ∠ AOC
b) Vì OB là phân giác của DOE nên ∠ BOD = ∠ BOE = 60\(^0\)
Ta có: ∠ BOC + ∠ BOE = ∠ COE
⇒ 30o + 60o = ∠ COE
⇒ ∠ COE = 90o
⇒ OC ⊥ OE ( đpcm )

Ta có hình vẽ:
A O B C D E
(vì kí hiệu AOC = BOD = 60o vào hình nhìn hơi rối nên mk ko kí hiệu nx nhé)
a)
- Ta có: AOC + BOC = AOB
=> 60o + BOC = 90o
=> BOC = 90o - 60o = 30o (1)
Lại có: BOC + COD = BOD
=> 30o + COD = 60o
=> COD = 60o - 30o = 30o (2)
Từ (1) và (2) => BOC = COD = 30o => OC là phân giác của BOD
- Ta có: COD + AOD = AOC
=> 30o + AOD = 60o
=> AOD = 60o - 30o = 30o
Vì COD = AOD = 30o nên OD là phân giác của AOC
b) Vì OB là phân giác của DOE nên \(BOD=BOE=60^o\)
Ta có: BOC + BOE = COE
=> 30o + 60o = COE
=> COE = 90o
\(\Rightarrow OC\perp OE\left(đpcm\right)\)

a) Vì tia OD nằm trong A O B ^ nên tia OD nằm giữa hai tia OA và OB do đó
A O D ^ + B O D ^ = A O B ^
Suy ra: A O D ^ = A O B ^ − B O D ^ = 90 0 − 60 0 = 30 0
Tương tự ta cũng có C O B ^ = 30 0 , D O C ^ = 30 0 .
b) Vì là tia phân giác của D O E ^ nên D O B ^ = B O E ^ = 60 0 .
Vì OB nằm giữa hai tia OC và OE và C O B ^ = 30 0 nên ta có
E O C ^ = E O B ^ + B O C ^ = 60 0 + 30 0 = 90 0
Vậy O C ⊥ O E