Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAOM và ΔBOM có:
+ Góc AOM = BOM.
+ OM là cạnh huyền chung.
+ Góc OAM = OBM = 90.
Nên ΔAOM = ΔBOM (ch-gn).
=>OM là đường trung trực của đoạn thẳng AB.
b) tam giác DMC là tam giác cân.
Xét ΔADM và ΔBCM có:
+ Góc MAD = MBC = 90.
+ Góc AMD = CMB (đối đỉnh).
+ AM = BM (ΔAOM = ΔBOM).
Nên ΔADM = ΔBCM (g.c.g).
=> DM = CM.
Nên ΔDMC là tam giác cân.
c) Ta có ΔDMC là tam giác cân, Nên DM + MC > DC.
Xét ΔADM có AM là cgv nên: AM< DM =>2AM < DC.
<=> AM + DM < DC

Em tham khảo tại link dưới đây nhé.
Câu hỏi của trần thị thúy vân - Toán lớp 7 - Học toán với OnlineMath

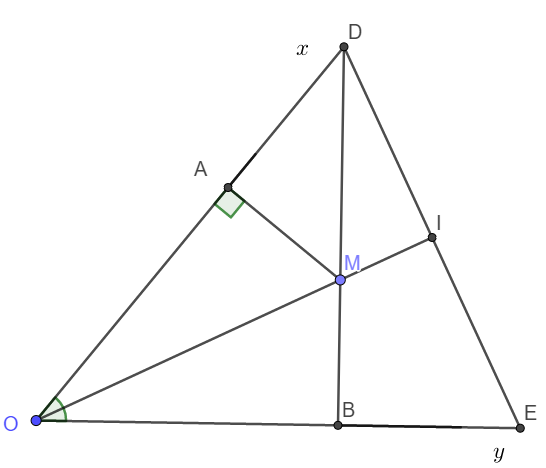
a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.