Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có :
OC vuông góc với OA = 90°
Mà OB' là phân giác A'OC
=> A'OB' = 90/2 = 45°
Mà OA là tia đối OA' (gt)
=> AOB = A'OB' = 45°
b) Vì B'OD = 90°
Mà A'OB' = 45°(cmt)
=> A'OD = 45°
=> A'OD = A'OB' = 45°
=> OA' là phân giác B'OD
Cho tam giác ABC, tia phân giác trong AD , M là điểm bất kì thuộc đường thẳng BC. Qua M vẽ đường thẳng song song với AD cắt AB,AC lần lượt tại P,Q. Chứng minh rằng tam giác APQ có hai góc bằng nhau
Bài 1
a
Ta có:
\(\widehat{O_1}=\widehat{O_2}=60^0\left(đ.đ\right)\)
\(\widehat{O_1}+\widehat{O_2}=180^0\Rightarrow\widehat{0_2}=180^0-\widehat{O_1}=180-60^0=120^0\)
\(\widehat{O_2}=\widehat{O_4}=120^0\left(đ.đ\right)\)
b
Ta có:
\(\widehat{x'Oy}=\widehat{y'Ox}\Rightarrow\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\widehat{y'Ox}\Rightarrow\widehat{yOn}=\widehat{xOm}\)
\(\widehat{x'Oy}+\widehat{yOx}=180^0\)
\(\Rightarrow2\cdot\widehat{yOn}+\widehat{yOx}=180^0\)
\(\Rightarrow\widehat{yOn}+\widehat{yOx}+\widehat{xOm}=180^0\)
\(\Rightarrowđpcm\)
Bài 2
a
Ta có:
\(\widehat{BOD}=\widehat{AOC}=90^0\Rightarrow\widehat{BOC}+\widehat{COD}=\widehat{AOD}+\widehat{COD}\Rightarrow\widehat{BOC}=\widehat{AOD}\)
b
Ta có:
\(\widehat{BOM}=\widehat{BOC}+\widehat{COM}=\widehat{AOD}+\widehat{MOD}=\widehat{MOA}\)
Hiển nhiên OM nằm giữa \(\widehat{AOB}\) nên suy ra đpcm
có góc AOB +góc BOA' =góc AOA'
mà góc AOA'= 90 độ ( OA' vuông góc vs OA)
=> góc AOB+ góc BOA'= 90 độ
có góc AOB+góc AOB'= gócBOB'
mà góc BOB'= 90 độ ( OB' vuông góc vs OB)
=> góc AOB + góc AOB'= 90 độ
có: góc AOB + góc A'OB' = góc AOB + (góc AOB' + góc AOB + góc A'OB)
= ( góc AOB + góc AOB') + ( góc AOB + góc A'OB)
mà góc AOB + góc AOB'= 90 độ ( cmt)
góc AOB+ góc A'OB= 90 độ (cmt )
=> góc AOB + góc A'OB' = 90 độ + 90 độ
= 180 độ ( đpcm)
a) Tia OM là tia phân giác của góc AOB nên
A
O
M
^
=
B
O
M
^
=
120
°
:
2
=
60
°
.
Ta có O C ⊥ O B ⇒ B O C ^ = 90 ° .
Tia OM nằm giữa hai tia OB, OC nên B O M ^ + C O M ^ = B O C ^
⇒ C O M ^ = 90 ° − 60 ° = 30 °
Tia OC nằm giữa hai tia OA, OB nên A O C ^ + B O C ^ = A O B ^
⇒ A O C ^ = 120 ° − 90 ° = 30 °
Vậy A O C ^ = C O M ^ = 30 ° . (1)
Tia OC nằm giữa hai tia OA, OM nên từ (1) suy ra tia OC là tia phân giác của góc AOM.
b) Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OA nằm giữa hai tia ON, OM nên A O N ^ + A O M ^ = M O N ^ .
Suy ra A O N ^ = M O N ^ − A O M ^ = 90 ° − 60 ° = 30 ° .
Vậy A O N ^ = A O C ^ = 30 ° (2)
Tia OA nằm giữa hai tia ON, OC nên từ (2) suy ra tia OA là tia phân giác của góc CON.
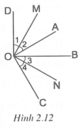
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .
Tia OB nằm giữa hai tia OA, OC.
Do đó A O B ^ + B O C ^ = 90 ° . (1)
Tương tự, ta có A O B ^ + A O D ^ = 90 ° . (2)
Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).
Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .
Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .
Vì A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .
Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .
Do đó M O N ^ = 90 ° ⇒ O M ⊥ O N