Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ngày mai tớ đi hok rùi
,huhu
,ai giỏi thì giúp tớ đi.anh chị CTV giỏi thì giúp em lun,mà nhớ vẽ hình rùi giải nha
Ta có hình vẽ: m O n A B x y z m n a
Vẽ tia Oz nằm trong góc mOn sao cho Oz // Ax
Ta có: mAx = mOz = mo (đồng vị)
Lại có: mOz + zOn = mOn
=> mo + zOn = ao
=> zOn = no
Do zOn = yBn = no
Mà zOn và yBn là 2 góc đồng vị => Oz // By
Mặt khác, Oz // Ax
=> Ax // By (đpcm)
Ta có : \(mOn=mDt\left(=60^0\right)\); mà hai góc này ở vị trí so le trong tạo bởi tia \(Om\) cắt tia \(Dt\) và \(On\)
⇒ \(Dt\) // \(On\) \(\left(DHNB\right)\)
Câu 2:
\(\dfrac{3^{3x}+3^{3x+2}}{3^3}=\dfrac{4^{2x+1}+4^{2x}}{2^3}\)
\(\Rightarrow\dfrac{3^{3x}\left(1+3^2\right)}{3^3}=\dfrac{4^{2x}\left(4^1+1\right)}{2^3}\)
\(\Rightarrow\dfrac{27^x.10}{27}=\dfrac{16^x.5}{8}\Rightarrow27^{x-1}.10=16^{x-1}.10\)
\(\Rightarrow27^{x-1}=16^{x-1}\)
Vì \(27\ne16\) và \(27;16\in N\)* nên
\(x-1=0\Leftrightarrow x=1\)
Vậy...................
Chúc bạn học tốt!!!
\(\left\{{}\begin{matrix}xy=-2\\yz=-3\\xz=6\end{matrix}\right.\) \(\Leftrightarrow xy.yz.xz=36\Leftrightarrow\left(xyz\right)^2=36\Leftrightarrow xyz=6\)
\(\Leftrightarrow\left\{{}\begin{matrix}z=-3\\x=-2\\x=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}z^2=9\\x^2=4\\x^2=1\end{matrix}\right.\)
\(\Leftrightarrow x^2+y^2+z^2=9+4+1=12\)
x y' y x' O N M Q P xét 2 tam giác \(\Delta NOP\) Và \(\Delta MOQ\) có :
\(NO=OM\) ( gt)
\(\widehat{NOP}=\widehat{MOQ}\) ( đối đỉnh )
\(OP=OQ\) ( GT)
\(\Rightarrow\Delta NOP=\Delta MOQ\left(C.G.C\right)\)
\(\Rightarrow\widehat{ONP}=\widehat{OMQ}\) ( 2 cạnh tương ứng )
mà 2 góc này ở vị trí so le trong
\(\Rightarrow NP\) // \(MQ\)
hình như chỗ này có vấn đề:
Trên tia Ox' lấy điểm M , trên tia Ox lấy điểm B sao cho O là trung điểm của đoạn thẳng MN
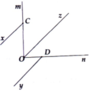
Kẻ Oz // Cx // Dy. Suy ra:
m O n ^ = C O z ^ + D O z ^ = O C x ^ + O D y ^
=> m O n ^ = 90°.