Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

Giải
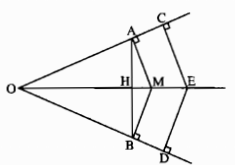
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

A B C M N Q P O R S T A B C H M D I A B C D K G M K E P F (Hình a) (Hình b) (Hình c) Q I
Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).

cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng
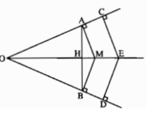

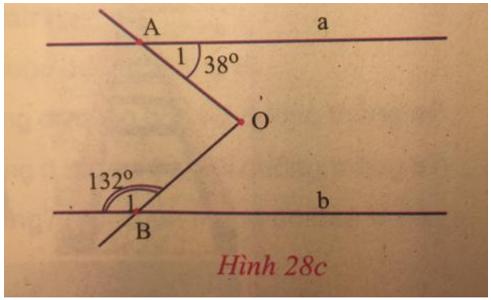
Gọi H là giao điểm của AB và OM.
Xét ΔAOM (vuông tại A) và ΔBOM (vuông tại B) có:
OM chung
∠MOA = ∠MOB ( vì OM là tia phân giác của góc xOy)
⇒ ΔAOM = ΔBOM (cạnh huyền – góc nhọn)
⇒ OA = OB.
+) Xét ΔOAH và ΔBOH có:
OA = OB ( chứng minh trên )
OH chung
∠AOH = ∠BOH ( vì OH là tia phân giác của góc xOy)
⇒ ΔOAH = ΔOBH (c.g.c)
⇒ ∠OHA = ∠OHB. Mà ∠OHA + ∠OHB = 180o ( hai góc kề bù)
⇒ ∠OHA = ∠OHB = 90o
Vậy AB ⊥ OM.