Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\widehat{AOB}=90^o\left(gt\right)\)
\(\widehat{AOC}=\widehat{BOD}\) (gt)
\(\Rightarrow\) \(\widehat{AOB}=\widehat{AOC}+\widehat{COB}=\widehat{BOD}+\widehat{COB}=90^O\) hay OC \(\perp\) OD

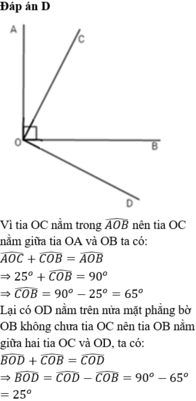
Ta có tia OC nằm trong góc AOB nên luôn có đẳng thức:
AOC+BOC=AOB=90
Theo đề bài thì AOC=BOD nên BOD+BOC=AOC+BOC=90
Nhưng chú ý rằng do OD nằm khác phía với OC qua OB nên hiển nhiên OB nằm trong COD
Cho nên BOC+BOD =COD
Do vậy COD=90 hay OC vuông góc với OD

Do mình không biết vẽ hình như nào nên mình sẽ chỉ giải bài thôi nhé , thoog cảm
Bài 1
Ta có \(\widehat{AOC}+\widehat{BOD}+\widehat{COD}=120^0\)
hay \(30^o+30^o+\widehat{COD}=120^o\)
\(\Rightarrow\widehat{COD}=120^o-30^o-30^o=60^o\)
Mà \(\widehat{AOC}+\widehat{COD}=30^o+60^o=90^o\)
Hay OA vuông góc với OD
Tương tự ta có OB vuông góc với OC
Vậy OA vuông góc với OD ; OB vuông góc với OC

O a b c d
Tia Od thuộc nửa mặt phẳng bờ Ob không chứa Oc
=> Tia Ob nằm trong ^cOd
=> ^cOd = ^cOb + ^bOd = ^cOb + ^ aOc = ^aOb = 90 độ.
=> Tia Oc và tia Od vuông góc với nhau.

bài 2:
góc moz = 1/2 góc xoz (1) (vì om là p/g của xoz)
góc noz = 1/2 góc yoz (2) (vì on là tia p/g của góc yoz)
từ (1) và(2) ta có : moz + noz = 1/2xoz + 1/2 yoz
moz + noz = 1/2 ( xoz + yoz)
moz + noz = 1/2. 180 độ
moz + noz = 90 độ x m z n y O
góc moz= 1/2 góc xoz(1) ( vÌ om là p/g của xoz)
gÓC noz= 1/2 góc yoz (2) ( vÌ on là tia p/g của góc yoz)
tu (1) va (2) ta co : moz + noz = 1/2xoz +1/2 yoz
moz + noz = 1/2 ( xỏr + yoz)
moz + noz = 1/2. 180 Đo
moz + noz = 90 do
chuppy moe sao lại là moz và noz người ta cho aob va aoc mà bạn giải thích giúp mình