Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

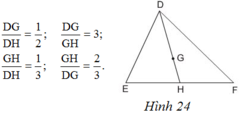
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Khẳng định đúng là:
GHDH=13GHDH=13 vì GHDG=23GHDG=23
nên DH−GHDH=3−23DH−GHDH=3−23
Tức là: GHDH=13GHDH=13

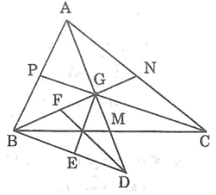
a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
b. Ta có: GM = MD (chứng minh trên)
Suy ra BM là đường trung tuyến của tam giác BGD.
Suy ra: BM = 1/2 BC (4)
Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:
FG = 1/2 BG (tính chất đường trung tuyến)
GN = 1/2 GB (tính chất đường trung tuyến)
Suy ra: FG = GN
Xét ΔDFG và ΔANG, ta có:
AG = GD (gt)
∠(DGF) = ∠(AGN) (đối đỉnh)
GF = GN (chứng minh trên)
Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN
Mà AN = 1/2 AC (gt)
Suy ra: DF = 1/2 AC (5)
Mặt khác: BD = CG (chứng minh trên)
ED = 1/2 BD (vì E là trung điểm BD)
GP = 1/2 CG (tính chất đường trung tuyến)
Suy ra: ED = GP
Lại có: ΔBMD = ΔCMG (chứng minh trên)
⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)
(CGM) = (PGA) (đối đỉnh)
Suy ra: ∠(EDG) = ∠(PGA)
AG = GD (gt)
Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)
Do đó: GE = 1/2 AB(6)
Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

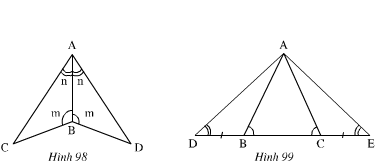
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

a) gọi AM,BN ,CH lần lượt là trung tuyến của tam giác ABC xuất phát từ các đỉnh A;B;C
Ta có BG=2/3BN( BN LÀ TRUNG TUYẾN CỦA TAM GIÁC ABC)
Ta có AG=2/3AM
=>GM=1/2AG
mà AG = GD
=> GM =MD= 1/2 GD
Xét tam giác GMC và DMB có :
GM=MD(cmt)
góc GMC=DMB (đối đỉnh)
BM=MC(gt)
=> 2 tam giác đó bằng nhau (c-g-c)
=>GC=BD (2-c-t-ứ) mà GC=2/3HC( vì CH là trung tuyến của tam giác ABC )=> BD=2/3CH
Ta có AG=2/3AM( AM là trung tuyến của tam giác ABC)
Mà AG=GD
=> GD=2/3AM


+ Vì G là trọng tâm của tam giác ABC có AD là một trung tuyến nên AG = 2/3AD, suy ra G không thể là trung điểm của AD => B sai
+ Vì AG = 2/3 AD => GD = 1/3 AD
Mà DM = 1/3 AD nên GD = DM
Mặt khác G thuộc tia DA, M thuộc tia đối của tia DA nên D nằm giữa M và G
Do đó D là trung điểm của MG, nên A đúng.


a) Ta có: f(-1)=1-8.(-1)=1+8=9
Vậy f(-1)=9 là đúng
b) Ta có: f(\(\frac{1}{2}\))=1-8.\(\frac{1}{2}\)=1-4=-3
Vậy f(\(\frac{1}{2}\))=-3 là đúng
c) Ta có: f(3)=1-8.3=1-24=-23
Vậy f(3)=25 là sai
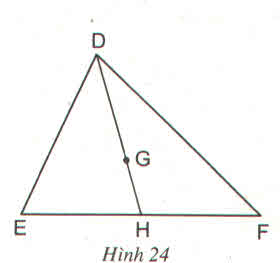






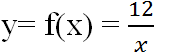

+ G là trọng tâm của tam giác DEF với đường trung tuyến DH.
Theo tính chất đường trung tuyến