Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)hình như đề sai thì phải
sửa lại
\(\left(\dfrac{1}{7}-\dfrac{2}{5}\right).\dfrac{2016}{2017}+\left(\dfrac{13}{7}+\dfrac{2}{5}\right).\dfrac{2016}{2017}\)
=\(\dfrac{2016}{2017}.\left(\dfrac{1}{7}-\dfrac{2}{5}+\dfrac{13}{7}+\dfrac{2}{5}\right)\)
=\(\dfrac{2016}{2017}.2=\dfrac{4032}{2017}\)

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)

1. đề bạn ghi rõ lại giúp mình đc ko r mình giải lại cho
2. Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x^2}{2.3^2}=\dfrac{y^2}{5^2}=\dfrac{2x^2-y^2}{18-25}=\dfrac{-28}{-7}=4\)
\(\dfrac{x}{3}=4\Rightarrow x=12\)
\(\dfrac{y}{5}=4\Rightarrow y=20\)
Vậy x=12 và y=20

a) \(0,75:4,5=\dfrac{1}{15}:\left(2x\right)\)
\(\Rightarrow\) \(\dfrac{1}{6}=\dfrac{1}{30}:x\)
\(\Rightarrow\) \(x=\dfrac{1}{5}\)
a. \(0,75:4,5=\dfrac{1}{15}:\left(2x\right)\)
\(\Leftrightarrow\dfrac{1}{15}:\left(2x\right)=0,75:4,5\)
\(\Rightarrow\dfrac{1}{15}:\left(2x\right)=\dfrac{1}{6}\)
\(\Rightarrow2x=\dfrac{1}{15}:\dfrac{1}{6}=\dfrac{2}{5}\)
\(\Rightarrow x=\dfrac{2}{5}:2=\dfrac{1}{5}\)
Vậy...
b. \(\dfrac{-5}{x-2}=\dfrac{3}{-9}\)
\(\Leftrightarrow\left(x-2\right).3=\left(-5\right).\left(-9\right)\)
\(\Rightarrow\left(x-2\right).3=45\)
\(\Rightarrow\left(x-2\right)=45:3=15\)
\(\Rightarrow x=15+2=17\)
Vậy...
c. \(\dfrac{-2}{3}:x=\dfrac{1}{2}:\dfrac{3}{4}\)
\(\Rightarrow\dfrac{-2}{3}:x=\dfrac{2}{3}\)
\(\Rightarrow x=\dfrac{-2}{3}:\dfrac{2}{3}=-1\)
Vậy...
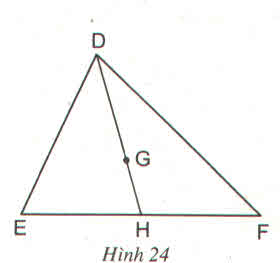
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Khẳng định đúng là:
GHDH=13GHDH=13 vì GHDG=23GHDG=23
nên DH−GHDH=3−23DH−GHDH=3−23
Tức là: GHDH=13GHDH=13
GH/DH=1/3