Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Áp dụng định lý về dấu của tam thức bậc 2.
a)
Để hàm \(f(x)=4x^2-(m+2)x+2m-3>0\forall x\in\mathbb{R}\)
\(\Leftrightarrow \Delta=(m+2)^2-16(2m-3)<0\)
\(\Leftrightarrow m^2-28m+52=(m-2)(m-26)<0\)
\(\Leftrightarrow 2< m<26\)
b)
Nếu \(m=-1\rightarrow f(x)=-6x\) không thể âm với mọi $x$
Nếu \(m\neq -1\):
Để \(f(x)=(m+1)x^2+2(2m-1)x-m-1<0\forall x\in\mathbb{R}\) thì cần hai đk sau:
1. \(m+1<0\leftrightarrow m<-1\)
2. \(\Delta'=(2m-1)^2+(m+1)^2<0\) (hiển nhiên vô lý)
Vậy không tồn tại $m$ thỏa mãn.

a) Ta có f'(x) = 6(x + 10)'.(x + 10)5
\(=6.\left(x+10\right)^5\)
f"(x) = 6.5(x + 10)'.(x + 10)4 = 30.(x + 10)4.
=> f''(2) = 30.(2 + 10)4 = 622 080.
b) Ta có f'(x) = (3x)'.cos3x = 3cos3x,
f"(x) = 3.[-(3x)'.sin3x] = -9sin3x.
Suy ra f"\(\dfrac{-\pi}{2}\) = -9sin\(\dfrac{-3\pi}{2}\) = -9;
f"(0) = -9sin0 = 0;
f"\(\dfrac{\pi}{18}\) = -9sin\(\dfrac{\pi}{6}\) = \(\dfrac{-9}{2}\).

a/ \(\frac{A^4_n}{A_{n+1}^3-C_n^{n-4}}=\frac{24}{23}\Rightarrow n=5\)
Khai triển \(\left(2-3x^2+x^3\right)^5\)
\(\left\{{}\begin{matrix}k_0+k_2+k_3=5\\2k_2+3k_3=9\end{matrix}\right.\) \(\Rightarrow\left(k_0;k_2;k_3\right)=\left(1;3;1\right);\left(2;0;3\right)\)
Hệ số của số hạng chứa \(x^9\):
\(\frac{5!}{1!.3!.1!}.2^1.\left(-3\right)^3+\frac{5!}{2!.3!}.2^2.\left(-3\right)^0=-1040\)
b/ SHTQ của khai triển: \(\left(1+2x\right)^n\) là: \(C_n^k2^kx^k\)
\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển tổng quát là \(C_n^32^3\)
\(\Rightarrow\) Hệ số của \(x^3\) trong khai triển của \(f\left(x\right)\): \(2^3.\sum\limits^{22}_{n=3}C_n^3\)
Tính tổng \(C_3^3+C_4^3+C_5^3+...+C_{22}^3\)
\(=C_4^4+C_4^3+C_5^3+...+C_{22}^3\)
\(=C_5^4+C_5^3+...+C_{22}^3\)
\(=C_6^4+C_6^3+...+C_{22}^3=...=C_{23}^4\)
Vậy \(2^3\sum\limits^{22}_{n=3}C_n^3=2^3.C_{23}^4\)

a/ \(f'\left(x\right)=2sinx.cosx-2sinx=0\)
\(\Leftrightarrow2sinx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=1\end{matrix}\right.\) \(\Rightarrow x=k\pi\)
b/ \(f'\left(x\right)=cosx+sin4x+sin6x=0\)
\(\Leftrightarrow cosx+2sin5x.cosx=0\)
\(\Leftrightarrow cosx\left(2sin5x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\sin5x=-\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\5x=-\frac{\pi}{6}+k2\pi\\5x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=-\frac{\pi}{30}+\frac{k2\pi}{5}\\x=-\frac{7\pi}{30}+\frac{k2\pi}{5}\end{matrix}\right.\)
Mình cảm ơn bạn, bạn có thể giúp mình làm thêm một số bài nữa được không ạ?

3.
\(SA\perp\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=\sqrt{AC^2+BC^2}=a\sqrt{3}\)
\(tan\widehat{SBA}=\frac{SA}{AB}=\frac{1}{\sqrt{3}}\Rightarrow\widehat{SBA}=30^0\)
4.
\(f'\left(x\right)=\frac{\left(x^2+3\right)'}{2\sqrt{x^2+3}}=\frac{x}{\sqrt{x^2+3}}\) \(\Rightarrow\left\{{}\begin{matrix}f\left(1\right)=2\\f'\left(1\right)=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=2+4.\frac{1}{2}=4\)
5.
Hàm \(y=\frac{3}{x^2+2}\) xác định và liên tục trên R
6.
\(\left\{{}\begin{matrix}k_1=f'\left(2\right)\\k_2=g'\left(2\right)\\k_3=\frac{f'\left(2\right).g\left(2\right)-g'\left(2\right).f\left(2\right)}{g^2\left(2\right)}\end{matrix}\right.\) \(\Rightarrow k_3=\frac{k_1.g\left(2\right)-k_2.f\left(2\right)}{g^2\left(2\right)}\Rightarrow\frac{1}{2}=\frac{g\left(2\right)-f\left(2\right)}{g^2\left(2\right)}\)
\(\Leftrightarrow g^2\left(2\right)=2g\left(2\right)-2f\left(2\right)\)
\(\Leftrightarrow1-2f\left(2\right)=\left[g\left(2\right)-1\right]^2\ge0\)
\(\Rightarrow2f\left(2\right)\le1\Rightarrow f\left(2\right)\le\frac{1}{2}\)
1.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=BC\)
\(BC=\sqrt{AC^2-AB^2}=a\)
2.
Qua S kẻ đường thẳng d song song AD
Kéo dài AM cắt d tại E \(\Rightarrow SADE\) là hình chữ nhật
\(\Rightarrow DE//SA\Rightarrow ED\perp\left(ABCD\right)\)
\(SBCE\) cũng là hcn \(\Rightarrow SB//CE\Rightarrow SB//\left(ACM\right)\Rightarrow d\left(SB;\left(ACM\right)\right)=d\left(B;\left(ACM\right)\right)\)
Gọi O là tâm đáy, BD cắt (ACM) tại O, mà \(BO=DO\)
\(\Rightarrow d\left(B;\left(ACM\right)\right)=d\left(D;\left(ACM\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp BD\\AC\perp ED\end{matrix}\right.\) \(\Rightarrow AC\perp\left(BDE\right)\)
Từ D kẻ \(DH\perp OE\Rightarrow DH\perp\left(ACM\right)\Rightarrow DH=d\left(D;\left(ACM\right)\right)\)
\(BD=a\sqrt{2}\Rightarrow OD=\frac{1}{2}BD=\frac{a\sqrt{2}}{2}\) ; \(ED=SA=2a\)
\(\frac{1}{DH^2}=\frac{1}{DO^2}+\frac{1}{ED^2}=\frac{9}{4a^2}\Rightarrow DH=\frac{2a}{3}\)
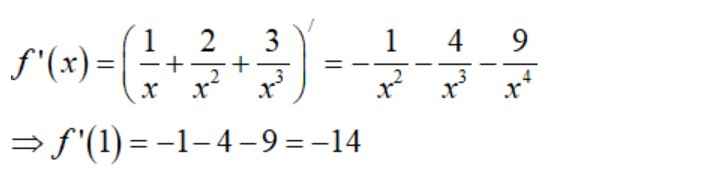
\(f\left(x\right)=x-\dfrac{1}{x}\Rightarrow f'\left(x\right)=1+\dfrac{1}{x^2}\); \(f''\left(x\right)=-\dfrac{2}{x^3}=\dfrac{\left(-1\right)^{2-1}.2!}{x^{2+1}}\) ;
\(f^{\left(3\right)}\left(x\right)=\dfrac{6}{x^4}=\dfrac{\left(-1\right)^{3-1}.3!}{x^{3+1}}\)
\(\Rightarrow f^{\left(n\right)}\left(x\right)=\dfrac{\left(-1\right)^{n-1}.n!}{x^{n+1}}\)