
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nguyên tắc để giải quyết vấn đề zigma luôn luôn là công thức chung.Cuối cùng, chúng ta phải chứng minh rằng số bắt đầu và số cuối cùng bằng nhau, sau đó tất cả các mẫu tính toán đều rất dễ dàng.
Được rồi, chúng ta hãy đến ví dụ đầu tiên (Violympic 8 - Round 10):
E x 1 :EX1: Hãy để một 1 , một 2 , . Tính tính tính Tính tính tính , Một nMột1,Một2,...,MộtN Được xác định bởi công thức:
A k = 3 k 2 + 3 k + 1 ( k 2 + k ) 3∀ k ≥ 1MộtK=3K2+3K+1(K2+K)3∀K≥1 Tìm tổng của: 1 + a 1 + a 2 + . Tính tính tính Tính tính tính + A 9 ?1+Một1+Một2+...+Một9?
Được rồi đây là một vấn đề dễ gây ra họ đã cho chúng ta tất cả các công thức và cuối cùng, số một.
Vì vậy, sử dụng máy tính: Chúng tôi sử dụng SHIFT + đăng nhập (ở trên ON):
Nó có vẻ như Σ x = ()ΣX=(), Nhập tất cả thông tin vào đó chúng ta có: 9 Σ 1 ( 3 x 2 + 3 x + 1 ( x 2 + x ) 3)Σ19(3X2+3X+1(X2+X)3) (Nhớ luôn sử dụng x để diễn tả). Gõ tất cả các thông tin sau đó nhấn "=" chúng ta có giải pháp 999 10009991000.
Số tiền là 1 + 999 1000= 1999 10001+9991000=19991000.
Dễ dàng phải không?
Bây giờ chúng ta đến ví dụ 2:
Tính: A = 1 1 + 2+ 1 1 + 2 + 3+ . Tính tính tính Tính tính tính + 1 1 + 2 + 3 + . Tính tính tính Tính tính tính + 99+ 1 50A=11+2+11+2+3+...+11+2+3+...+99+150?
Vì vậy chúng ta tạo ra công thức tổng quát là n 2⋅ ( n + 1 )N2⋅(N+1)Tính tính tính (Công thức này bạn phải có nếu không chúng ta không thể sử dụng máy tính). Vì vậy, công thức chung là: 1 n 2( N + 1 )1N2(N+1)
Vì vậy, chúng tôi tiếp tục sử dụng máy tính để gõ: D: 99 Σ x = 2 ⎛ ⎜ ⎝ 1 x 2⋅ ( x + 1 )⎞ ⎟ ⎠ΣX=299(1X2⋅(X+1)) Chúng ta có câu trả lời: 49 504950
Vì vậy, câu trả lời là 49 50+ 1 50= 14950+150=1. Dễ dàng phải không?
Bây giờ chúng ta gặp vấn đề khó khăn hơn như sau:
Ví dụ 3: A = 2014 + 2013 2+ 2012 3+ . Tính tính tính Tính tính tính + 2 2013+ 1 20141 2+ 1 3+ 1 4+ . Tính tính tính Tính tính tính + 1 2015A=Năm 2014+Năm 20132+Năm 20123+...+2Năm 2013+1Năm 201412+13+14+...+12015
Tìm công thức chung của tử số là ( 2015 - x ) x(2015-X)X
Vì vậy hãy tính số tử chúng ta có: 2014 Σ x = 1 ( 2015 - x x) = 14.479 , 46.409ΣX=1Năm 2014(2015-XX)=14479,46409 => Đừng lo lắng về câu trả lời, giữ nó ở đó.
Bây giờ chúng ta tính đến mẫu số chung với công thức là 1 x1X
Chúng tôi có 2014 Σ x = 1 ( 1 x) = 7 , 185838258ΣX=1Năm 2014(1X)=7,185838258
Bây giờ câu trả lời là tử số / mẫu số = 14.479 , 46.409 7 , 185.838.258= 201514479,464097,185838258=2015 => Câu trả lời cuối cùng là một số đẹp.

Bài 1:
Xét ΔABC vuông tại A có
\(\cos B=\dfrac{AB}{BC}\)
nên \(BC=3:\cos60^0=6\left(cm\right)\)
=>\(AC=3\sqrt{3}\left(cm\right)\)

a. \(\sqrt{4x}+\sqrt{x}=2\Leftrightarrow2\sqrt{x}+\sqrt{x}=2\Leftrightarrow3\sqrt{x}=2\Leftrightarrow\sqrt{x}=\frac{2}{3}\Leftrightarrow x=\frac{4}{9}\)
b. \(\sqrt{x^2-4}=\sqrt{x-2}\Leftrightarrow\hept{\begin{cases}x^2-4=x-2\\x-2\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}\orbr{\begin{cases}x=2\\x=-1\end{cases}}\\x\ge2\end{cases}}\Leftrightarrow x=2\)\(\sqrt{x^2-4}=\sqrt{x-2}\Leftrightarrow\hept{\begin{cases}x^2-4=x-2\\x-2\ge2\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(x-2\right)\left(x+1\right)=0\\x\ge2\end{cases}}\Leftrightarrow x=2\)
c.\(\sqrt{x^2-2x}+\sqrt{2x^2+4x}=2x\Leftrightarrow\hept{\begin{cases}x\ge0\\x^2-2x+2x^2+4x+2\sqrt{x^2-2x}.\sqrt{2x^2+4x}=4x^2\end{cases}}\)
\(\Rightarrow x^2-2x=2\sqrt{x^2-2x}.\sqrt{2x^2+4x}\Leftrightarrow\orbr{\begin{cases}\sqrt{x^2-2x}=0\\\sqrt{x^2-2x}=2\sqrt{2x^2+4x}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\text{ hoặc }x=2\\x^2-2x=8x^2+16x\end{cases}\Leftrightarrow}\)hoặc x=0 hoặc x=2 hoặc x= -18/7
Kết hợp điều kiện ta có : \(x=0\text{ hoặc }x=2\)
d. Điều kiện \(x\ge3\) ta có :
\(\sqrt{x^2+2x-15}=\sqrt{x-3}+\sqrt{x^2-3x}\Leftrightarrow x^2+2x-15=x^2-2x-3+2\sqrt{x-3}\sqrt{x^2-3x}\)
\(\Leftrightarrow2x-6=\sqrt{x-3}.\sqrt{x^2-3x}\Leftrightarrow4\left(x-3\right)^2=\left(x-3\right)\left(x^2-3x\right)\Leftrightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)

Nhiều quá :v
f)\(\left(x^2+y^2\right)2\ge\left(x+y\right)^2\)( BĐT Bunyakovsky)
\(\Rightarrow\sqrt{2}\ge x+y\)
h) \(\dfrac{3-4x}{x^2+1}=\dfrac{x^2-4x+4-x^2-1}{x^2+1}=\dfrac{\left(x-2\right)^2}{x^2+1}-1\ge-1\)
\(\dfrac{3-4x}{x^2+1}=\dfrac{4x^2+4-4x^2-4x-1}{x^2+1}=4-\dfrac{\left(2x+1\right)^2}{x^2+1}\le4\)
g) Làm tương tự bài trên hoặc kiểu này
Đặt \(y_o=\dfrac{x^2-x+1}{x^2+x+1}\)
Rồi tính Delta rồi tìm Min,Max

a)\(\sqrt{x+1}-\sqrt{x-2}=1\)
Đk:\(x\ge2\)
\(pt\Leftrightarrow\left(\sqrt{x+1}-2\right)-\left(\sqrt{x-2}-1\right)=0\)
\(\Leftrightarrow\dfrac{x+1-4}{\sqrt{x+1}+2}-\dfrac{x-2-1}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{x+1}+2}-\dfrac{x-3}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{x+1}+2}-\dfrac{1}{\sqrt{x-2}+1}\right)=0\)
Dễ thấy:\(\dfrac{1}{\sqrt{x+1}+2}-\dfrac{1}{\sqrt{x-2}+1}< 0\)
Nên \(x-3=0\Rightarrow x=3\)
b)\(\sqrt{x-1}-\sqrt{5x-1}=\sqrt{3x-2}\)
Đk:\(x\ge1\)
\(pt\Leftrightarrow\sqrt{x-1}=\sqrt{5x-1}+\sqrt{3x-2}\)
\(\Leftrightarrow x-1=5x-1+3x-2+2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow2-7x=2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow49x^2-28x+4=4\left(5x-1\right)\left(3x-2\right)\)
\(\Leftrightarrow49x^2-28x+4=60x^2-52x+8\)
\(\Leftrightarrow-11x^2+24x-4=0\Leftrightarrow\left(2-x\right)\left(11x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{2}{11}\end{matrix}\right.\) (loại hết)
c)\(\sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0\)
Đk:\(x\ge0\)
\(pt\Leftrightarrow\sqrt{x}-\left(\sqrt{x+1}+1\right)-\left(\sqrt{x+4}+2\right)+\left(\sqrt{x+9}-3\right)=0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{x+1-1}{\sqrt{x+1}+1}-\dfrac{x+4-4}{\sqrt{x+4}+2}+\dfrac{x+9-9}{\sqrt{x+9}-3}=0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{x}{\sqrt{x+1}+1}-\dfrac{x}{\sqrt{x+4}+2}+\dfrac{x}{\sqrt{x+9}-3}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x+1}+1}-\dfrac{1}{\sqrt{x+4}+2}+\dfrac{1}{\sqrt{x+9}-3}\right)=0\)
Dễ thấy:\(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x+1}+1}-\dfrac{1}{\sqrt{x+4}+2}+\dfrac{1}{\sqrt{x+9}-3}>0\)
Nên \(x=0\)
Cho +
+  = \frac{1}{a+b} ;
= \frac{1}{a+b} ;  . CMR
. CMR
 +
+  =
= 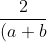%5E1000%7D)
a)
b)
Cho +
+  = \frac{1}{a+b} ;
= \frac{1}{a+b} ;  . CMR
. CMR
a)
b) +
+  =
= 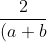%5E1000%7D)
lưu ý chép kĩ nhé nguyenchieubao
nguyenchieubao
ai k cho mk thì mk cho lại