Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(f\left(x\right)=x.e^x\)
\(f'\left(x\right)=e^x+x.e^x\)
\(f"\left(x\right)=e^x+e^x+x.e^x=2e^x+x.e^x\)
\(f^{\left(3\right)}\left(x\right)=2e^x+e^x+x.e^x=3e^x+x.e^x\)
b.Từ (a) ta đi đến công thức (dự đoán)
\(f^{\left(n\right)}\left(x\right)=ne^x+x.e^x\) (1)
Chứng minh (1) bằng quy nạp như sau :
- (1) đã đúng với \(n=1,2,3\)
- Giả sử (1) đã đúng đến n, ta phải chứng minh :
\(f^{\left(n+1\right)}\left(x\right)=\left(n+1\right)e^x+x.e^x\) (2)
Thật vậy , từ giả thiết quy nạp, ta có :
\(f^{\left(n+1\right)}\left(x\right)=\left(f^{\left(n\right)}\left(x\right)\right)'=\left(ne^x+x.e^x\right)'=ne^x+e^x+x.e^x=\left(n+1\right)e^x+x.e^x\)
Vậy (2) đúng. Theo nguyên lí quy nạp suy ra (1) đúng với mọi \(n=1,2,3....\)
Tóm lại, ta có với mọi \(n=1,2,3....\)
\(f^{\left(n\right)}\left(x\right)=ne^x+x.e^x\)

a) Ta có f'(x) = 6(x + 10)'.(x + 10)5
\(=6.\left(x+10\right)^5\)
f"(x) = 6.5(x + 10)'.(x + 10)4 = 30.(x + 10)4.
=> f''(2) = 30.(2 + 10)4 = 622 080.
b) Ta có f'(x) = (3x)'.cos3x = 3cos3x,
f"(x) = 3.[-(3x)'.sin3x] = -9sin3x.
Suy ra f"\(\dfrac{-\pi}{2}\) = -9sin\(\dfrac{-3\pi}{2}\) = -9;
f"(0) = -9sin0 = 0;
f"\(\dfrac{\pi}{18}\) = -9sin\(\dfrac{\pi}{6}\) = \(\dfrac{-9}{2}\).

Ta có \(f\left(x\right)=\sin ax\)
\(f'\left(x\right)=a\cos ax=a\sin\left(ax+\frac{\pi}{2}\right)\)
\(f''\left(x\right)=a^2\cos\left(ax+\frac{\pi}{2}\right)=a^2\sin\left(ax+\frac{\pi}{2}+\frac{\pi}{2}\right)\)
\(f'''\left(x\right)=a^3\cos\left(ax+\pi\right)=a^3\sin\left(ax+\pi+\frac{\pi}{2}\right)=a^3\sin\left(ax+\frac{3\pi}{2}\right)\)
Dự đoán \(f^{\left(n\right)}\left(x\right)=a^n\sin\left(ax+\frac{n\pi}{2}\right)\left(1\right)\)
(1) được chứng minh bằng quy nạp như sau :
- (1) đúng khi n = 1,2,2
- Giả sử (1) đã đúng đến n. Ta phải chứng minh
\(f^{\left(n+1\right)}\left(x\right)=a^{n+1}\sin\left(ax+\frac{\left(n+1\right)\pi}{2}\right)\)
Theo giả thiết quy nạp ta có :
\(f^{\left(n+1\right)}\left(x\right)=\left(f^{\left(n\right)}\left(x\right)\right)'=\left(a^n\sin\left(ax+\frac{n\pi}{2}\right)\right)=a^n.a\cos\left(ax+\frac{n\pi}{2}\right)=a^{n+1}\sin\left(ax+\frac{n\pi}{2}+\frac{n\pi}{2}\right)=a^{n+1}\sin\left(ax+\frac{\left(n+1\right)\pi}{2}\right)\)
Vậy (2) đúng.
Theo nguyên lý quy nạp suy ra (1) đúng.
Như vậy ta có :
\(f^{\left(n\right)}\left(x\right)=a^n\sin\left(ax+\frac{n\pi}{2}\right)\)

Theo định nghĩa ta có :
\(f'\left(x\right)=\lim\limits_{\Delta x\rightarrow0}\frac{f\left(a+\right)-f\left(a\right)}{\Delta x}\)
\(=\lim\limits_{\Delta x\rightarrow0}\frac{\left(a+\Delta x-1\right)\varphi\left(a+\Delta x\right)}{\Delta x}\) do (\(f\left(a\right)=0\))
\(=\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)\)
Khi \(\Delta x\rightarrow0\) thì \(a+\Delta x\rightarrow a\) và do \(\varphi\left(x\right)\) là hàm liên tục tại x = a nên có :
\(\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)=\varphi\left(a\right)\)
Vậy \(f'\left(a\right)=\varphi\left(a\right)\)

Đáp án A
Đó là nguyên lý của giới hạn kẹp
\(\left|f\left(x\right)\right|\le\left|x\right|\Rightarrow\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}x=0\)

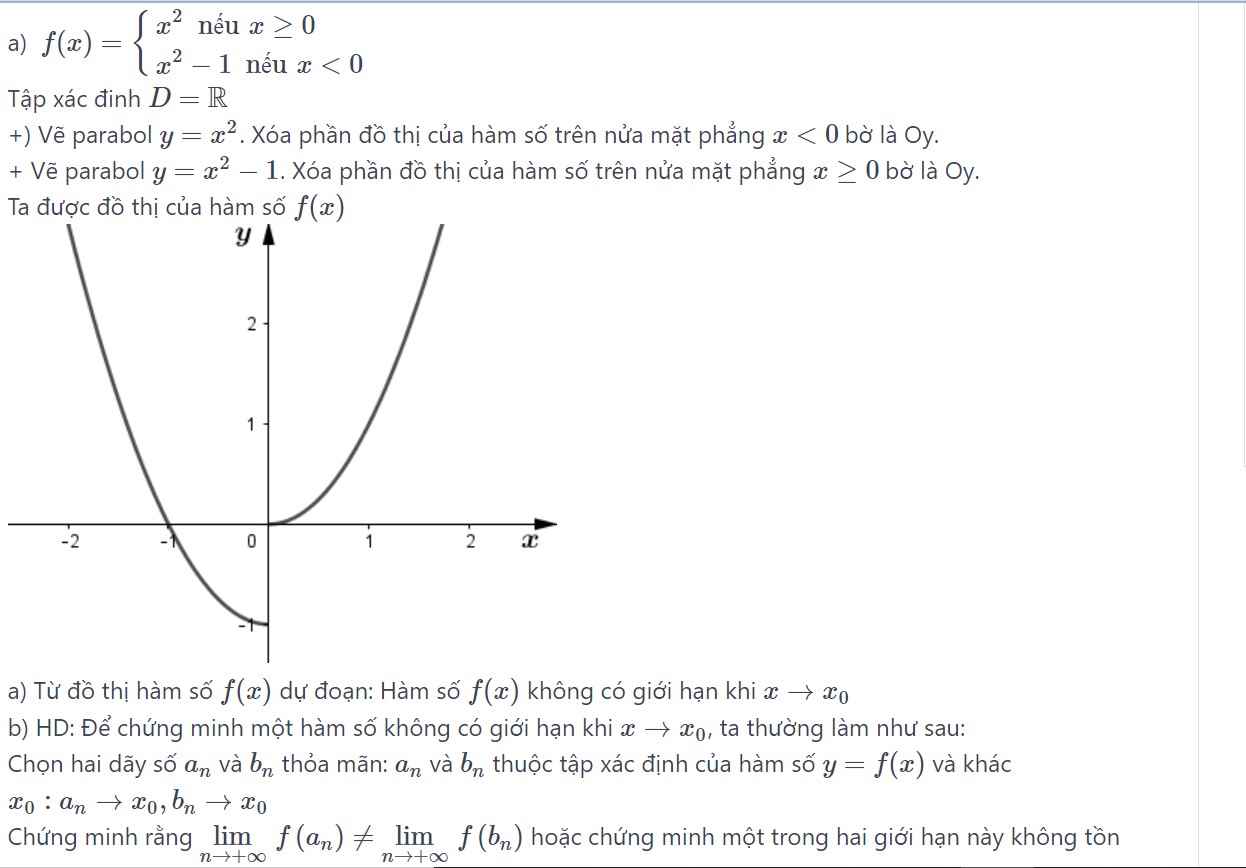
Đáp án B, do giới hạn trái tại 0 bằng âm vô cùng, giới hạn phải tại 0 bằng dương vô cùng
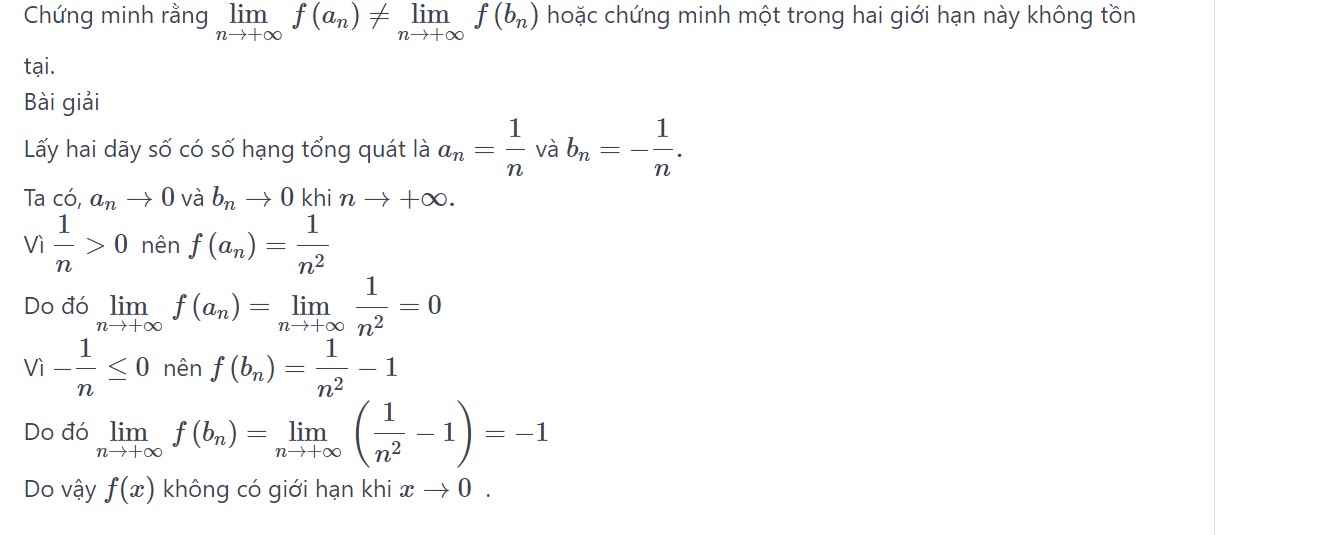
a. Ta có \(f'\left(x\right)=\ln x+x.\frac{1}{x}+\ln x\)
\(f"\left(x\right)=\frac{1}{x}\)
\(f'''\left(x\right)=-\frac{1}{x^2}\)
\(f^{\left(4\right)}\left(x\right)=\frac{2}{x^3}\)
b. Tương tự ta có :
\(f^{\left(5\right)}\left(x\right)=-\frac{2.3}{x^4}\)
\(f^{\left(6\right)}\left(x\right)=\frac{2.3.4}{x^5}\)
Từ đó suy ra \(f^{\left(5\right)}\left(x\right)=\left(-1\right)^n\frac{\left(n-2\right)!}{x^{n-1}}\) với \(n\ge2\)
Thật vậy, ta sẽ thấy công thức đúng khi n=2,3,4,......