Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta xét : \(f\left(x\right)+f\left(1-x\right)=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{1-3\left(1-x\right)+3\left(1-x\right)^2}\)
\(=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{3x^2-3x+1}=\frac{\left(x+1-x\right)\left(x^2+x^2-2x+1+x^2-x\right)}{3x^2-3x+1}=\frac{3x^2-3x+1}{3x^2-3x+1}=1\)
Áp dụng ta có :
\(A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1006}{2012}\right)+f\left(\frac{1006}{2012}\right)\right]\)
\(=1+1+...+1\)(Có tất cả 1006 số 1)
\(=1006\)

Đễ dàng chưng minh được
\(f\left(1-x\right)=1-f\left(x\right)\)
\(\Rightarrow f\left(1-x\right)+f\left(x\right)=1\)
\(\Rightarrow A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1005}{2012}\right)+f\left(\frac{1007}{2012}\right)\right]+f\left(\frac{1006}{2012}\right)\)
\(=1005+f\left(\frac{1006}{2012}\right)\)
Làm nôt

Lời giải:
Ta thấy: \(f(x)=\frac{x^3}{1-3x+3x^2}\Rightarrow f(1-x)=\frac{(1-x)^3}{1-3(1-x)+3(1-x)^2}=\frac{(1-x)^3}{3x^2-3x+1}\)
\(\Rightarrow f(x)+f(1-x)=\frac{x^3}{1-3x+3x^2}+\frac{(1-x)^3}{3x^2-3x+1}=\frac{x^3+(1-x)^3}{3x^2-3x+1}=1\)
Do đó:
\(f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)=1\)
\(f\left(\frac{2}{2017}\right)+f\left(\frac{2015}{2017}\right)=1\)
............
\(f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)=1\)
Cộng theo vế:
\(\Rightarrow A=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+f\left(\frac{3}{2017}\right)+...f\left(\frac{2015}{2017}\right)+f\left(\frac{2016}{2017}\right)\)
\(=\underbrace{1+1+1...+1}_{1008}=1008\)

a: \(=\dfrac{1}{x-y}\cdot x^2\cdot\left(x-y\right)=x^2\)
b: \(=\sqrt{27\cdot48}\cdot\left|a-2\right|=36\left(a-2\right)\)
c: \(=\left(\sqrt{2012}+\sqrt{2011}\right)^2\)
d: \(=\dfrac{8}{7}\cdot\dfrac{-x}{y+1}\)
e: \(=\dfrac{11}{12}\cdot\dfrac{x}{-y-2}=\dfrac{-11x}{12\left(y+2\right)}\)

c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Các hàm số y = f(x) = 2/3 x và y = g(x) = 2/3 x + 3 là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
a) Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x\)
Ta có : \(f\left(-2\right)=\dfrac{2}{3}.\left(-2\right)=-\dfrac{4}{3}\)
\(f\left(-1\right)=\dfrac{2}{3}.\left(-1\right)=-\dfrac{2}{3}\)
\(f\left(0\right)=\dfrac{2}{3}.0=0\)
\(f\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)
\(f\left(1\right)=\dfrac{2}{3}.1=\dfrac{2}{3}\)
\(f\left(2\right)=\dfrac{2}{3}.2=\dfrac{4}{3}\)
\(f\left(3\right)=\dfrac{2}{3}.3=2\)
b) Cho hàm số : \(y=g\left(x\right)=\dfrac{2}{3}x+3\)
\(g\left(-2\right)=\dfrac{2}{3}.\left(-2\right)+3=\dfrac{5}{3}\)
\(g\left(-1\right)=\dfrac{2}{3}.\left(-1\right)+3=\dfrac{7}{3}\)
\(g\left(0\right)=\dfrac{2}{3}.0+3=3\)
\(g\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}+3=\dfrac{10}{3}\)
\(g\left(1\right)=\dfrac{2}{3}.1+3=\dfrac{11}{3}\)
\(g\left(2\right)=\dfrac{2}{3}.2+3=\dfrac{13}{3}\)
\(g\left(3\right)=\dfrac{2}{3}.3+3=5\)
c) Khi \(x\)lấy cùng một giá trị thì giá trị của \(g\left(x\right)\) lớn hơn giá trị của \(f\left(x\right)\) là \(3\) đơn vị.

Bài 1:
Đặt \(\left\{\begin{matrix} 5x+3=a\\ 2x+4=b\end{matrix}\right.\) \(\Rightarrow 3x-1=a-b\)
PT trở thành:
\(a^3-b^3=(a-b)^3\)
\(\Leftrightarrow (a-b)(a^2+ab+b^2)=(a-b)^3\)
\(\Leftrightarrow (a-b)[a^2+ab+b^2-(a^2-2ab+b^2)]=0\)
\(\Leftrightarrow 3ab(a-b)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=0\\b=0\\a=b\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{5}\\x=-2\\5x+3=2x+4\Leftrightarrow x=\dfrac{1}{3}\end{matrix}\right.\)
Thử lại thấy đều thỏa mãn
Vậy \(x\in\left\{\frac{-3}{5};-2;\frac{1}{3}\right\}\)
Bài 2:
\(\frac{x-1}{2013}+\frac{x-2}{2012}-\frac{x-3}{2011}=\frac{x-4}{2010}\)
\(\Leftrightarrow \frac{x-1}{2013}-1+\frac{x-2}{2012}-1-\left(\frac{x-3}{2011}-1\right)=\frac{x-4}{2010}-1\)
\(\Leftrightarrow \frac{x-2014}{2013}+\frac{x-2014}{2012}-\frac{x-2014}{2011}=\frac{x-2014}{2010}\)
\(\Leftrightarrow (x-2014)\left(\frac{1}{2013}+\frac{1}{2012}-\frac{1}{2011}-\frac{1}{2010}\right)=0\) (1)
Thấy rằng \(2013> 2011; 2012> 2010\Rightarrow \frac{1}{2013}< \frac{1}{2011}; \frac{1}{2012}< \frac{1}{2010}\)
\(\Rightarrow \frac{1}{2013}+\frac{1}{2012}-\frac{1}{2011}-\frac{1}{2010}< 0\) (2)
Từ (1),(2) suy ra \(x-2014=0\Leftrightarrow x=2014\)
Bài 3:
Đặt \(\left\{\begin{matrix} 2x-5=a\\ x-2=b\end{matrix}\right.\Rightarrow x-3=a-b\)
PT trở thành: \(a^3-b^3=(a-b)^3\)
\(\Leftrightarrow (a-b)(a^2+ab+b^2)-(a-b)(a^2-2ab+b^2)=0\)
\(\Leftrightarrow 3ab(a-b)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=0\\b=0\\a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=2\\x-3=0\Leftrightarrow x=3\end{matrix}\right.\)
Vậy \(x\in\left\{\frac{5}{2}; 2; 3\right\}\)

1.
Nhân 2 vế của BĐT với \(\left(a+b+c\right)\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(3(a^2+b^2+c^2)(a+b)(b+c)(c+a)\ge(a+b+c)\left(Σ_{cyc}(a^2+b^2)(c+a)(c+b)\right)\)
\(\LeftrightarrowΣ_{perms}a^2b\left(a-b\right)^2\ge0\) *đúng*
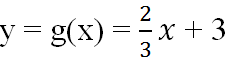
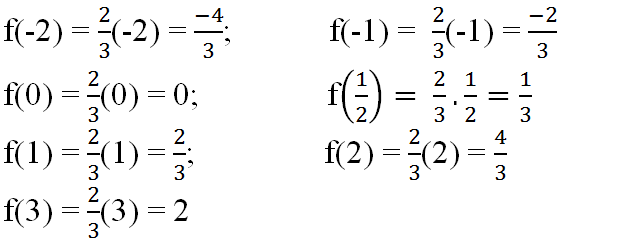
Bạn kiểm tra lại đề, \(f\left(x\right)=\dfrac{x^3}{1-3x-3x^2}\) hay \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\)