Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C.
Vì lnC mới là số thực tùy ý, D sai vì không cộng hằng số C vào biến.

Đáp án: C.
Vì lnC mới là số thực tùy ý, D sai vì không cộng hằng số C vào biến.

Theo tính chất của tích phân:
\(\int\limits^4_1f'\left(x\right)dx=f\left(4\right)-f\left(1\right)\Rightarrow f\left(4\right)-f\left(1\right)=17\)
\(\Rightarrow f\left(4\right)=f\left(1\right)+17=-12+17=5\)

\(y'=\frac{5\left(x^2+4\right)-2x.5x}{\left(x^2+4\right)}f'\left(\frac{5x}{x^2+4}\right)=\frac{5\left(4-x^2\right)}{x^2+4}f'\left(\frac{5x}{x^2+4}\right)\)
\(=\frac{5\left(2-x\right)\left(2+x\right)}{\left(x^2+4\right)}.\left(\frac{5x}{x^2+4}\right)^2.\left(\frac{5x}{x^2+4}-1\right)\left(\frac{65x}{x^2+4}-15\right)^3\)
\(=\frac{5\left(2-x\right)\left(2+x\right).25x^2\left(x-4\right)\left(1-x\right)\left(x-3\right)^3\left(4-3x\right)^3.5^3}{\left(x^2+4\right)^7}\)
Ta thấy \(y'=0\) có 7 nghiệm nhưng nghiệm \(x=0\) có mũ chẵn nên hàm số có 6 điểm cực trị

Ta có f ( 0 ) = 0 f ( 1 ) = 0 f ' ( 0 ) = 0 f ' ( 1 ) = 0
↔ a = 2 b = - 3 c = 0 d = 1
, suy ra hàm số đã cho là : y= 2x3-3x2+ 1.
Ta thấy: f(x) = 0 ↔ x = 0 hoặc x = -1/2
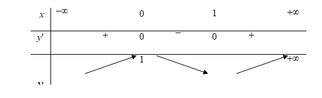
Bảng biến thiên của hàm số y = |f(x)| như sau:
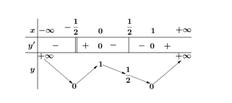
Dựa vào bảng biến thiên suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x1< x2< x3< ½< x4 khi và chỉ khi ½< m< 1.
Chọn A.
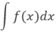 bằng:
bằng: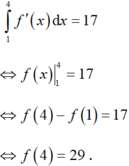
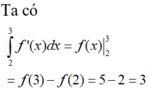
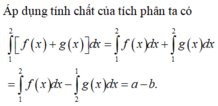
Chọn C.
Vì x = 2,7 > 0 nên ta có:
do đó: f( 2,7) = 2,7.