Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số đường chéo của đa giác đó :
\(\frac{\left(8-3\right).8}{2}=20\)( đường chéo )
b) Tổng số đo các góc của đa giác là :
\(108.\left(8-2\right)=108.6=1080\)độ
c) Số đo mỗi góc của đa giác đều 8 cạnh :
\(1080:8=135\)độ

Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là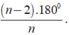
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
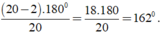
+ Số đường chéo của đa giác n cạnh là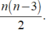
Khi đó số đường chéo của đa giác đều 20 cạnh là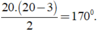

cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.

Xét đa giác có n cạnh hay n góc
1
a) Một góc trong tạo với 1 góc ngoài kề với nó tạo ra 1 góc bẹt => Có n góc bẹt, tổng chúng là 1800n
Ta có tổng các góc trong đa giác có n góc là (n−2)1800(n−2)1800
=> tổng các góc ngoài là 1800n - (n−2)1800(n−2)1800 = 3600
b.Ta có số đường chéo của đa giác n cạnh là \(\frac{n\left(n-3\right)}{2}\)
Ta có: 3n= \(\frac{n\left(n-3\right)}{2}\) ⇔6n=n(n−3)⇔6=n−3⇔n=9
Một góc trong tạo với 1 góc ngoài kề với nó tạo ra 1 góc bẹt => Có n góc bẹt, tổng chúng là 1800n
Ta có tổng các góc trong đa giác có n góc là (n - 2) 180
=> tổng các góc ngoài là 180on - (n - 2) 180 = 3600
Ta có số đường chéo của đa giác n cạnh là:\(\frac{n\left(n-3\right)}{2}\)
Ta có : \(3n=\frac{n\left(n-3\right)}{2}\Leftrightarrow6n=n\left(n-3\right)\Leftrightarrow6=n-3\Rightarrow n=9\)

Gọi số cạnh là n
Ta có công thức tính mỗi góc của đa giác đều n cạnh là :
\(\frac{\left(n-2\right).180^0}{n}\)
Đa giác đều có số đường chéo bằng số cạnh
\(\Rightarrow\)Đa giác đều đó là tam giác đều và tổng số đo mỗi góc là \(60^o\)

hình như toàn chép bài nhau thì phải
Gọi n là số cạnh của đa giác.
Ta có :
- Số đường chéo của đa giác là : n(n−3)2
Cái này dễ chứng minh thôi bn!
Từ mỗi đỉnh của hình n giác lồi ta vẽ được n - 1 đoạn thẳng nối đỉnh đó với n - 1 đỉnh còn lại, trong đó có 2 đoạn thẳng trùng với 2 cạnh của đa giác. Vậy qua mỗi đỉnh của hình n giác lồi vẽ được n - 3 đường chéo, hình n giác có n đỉnh nên vẽ được n(n - 3) đường chéo, trong đó mỗi đường chéo được tính 2 lần nên thực chất chỉ có n(n−3)2 đường chéo.
- Tổng số đo các góc trong đa giác : 180o.(n−2)
Còn số cạnh của đa giác thì tự đếm ra, nếu đề bài cho 1 số gt bắt tìm số cạnh thì dựa vào công thức tính đường chéo hay công thức tính số đo 1 góc đa giác đều (180o.(n−2)n.
Số đường chéo xuất phát từ mỗi đỉnh của đa giác n cạnh là n - 3.
__________________