
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cho tập hợp A=( -2;4), B=( -3;5). Tìm các tập hợp A giao B?

a: ΔOCB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc CB
Vì góc OIA=góc OMA=góc ONA
nên O,M,N,I,A cùng thuộc 1 đường tròn
b: Xét ΔABN và ΔANC có
góc ABN=góc ANC
góc BAN chung
=>ΔABN đồng dạng với ΔANC
=>AB/AN=AN/AC
=>AN^2=AB*(AB+BC)
=>4*(BC+4)=6^2=36
=>BC=5cm

\(a,\Leftrightarrow5x-3=4\Leftrightarrow x=\dfrac{12}{5}\\ b,ĐK:x\ge0\\ PT\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}+6=4\sqrt{x}+30\\ \Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ c,ĐK:x\ge-2\\ PT\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-15=2\sqrt{x+2}+12\\ \Leftrightarrow9\sqrt{x+2}=27\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\\ \Leftrightarrow x=7\left(tm\right)\\ d,\Leftrightarrow\left|x\right|=13\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-13\end{matrix}\right.\)
a: \(\Leftrightarrow5x-3=4\)
hay \(x=\dfrac{7}{5}\)

1: Thay x=25 vào A, ta được:
\(A=\dfrac{5-3}{2\cdot5+6}=\dfrac{2}{16}=\dfrac{1}{8}\)
2: \(B=\dfrac{x+16-5\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)

Câu 7:
b: Tọa độ của C là:
\(\left\{{}\begin{matrix}2x-3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow C\left(4;5\right)\)

\(c,\text{PTHĐGD }y=x+1\text{ và }\left(d\right):\\ x+1=2x-3\\ \Leftrightarrow x=4\Leftrightarrow y=5\Leftrightarrow A\left(4;5\right)\\ \text{Để 3 đt đồng quy }\Leftrightarrow A\left(4;5\right)\in y=\left(m-1\right)x+5\\ \Leftrightarrow4m-4+5=5\\ \Leftrightarrow m=1\)

Bài 2:
b. \(\sqrt{\left(3x+1\right)^2}=25\)
<=> \(|3x+1|=25\)
<=> \(\left[{}\begin{matrix}3x+1=-25\\3x+1=25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-26}{3}\\x=8\end{matrix}\right.\)
Bài 3:
Ta có: \(\dfrac{5}{\sqrt{7}+\sqrt{2}}+\dfrac{2}{3+\sqrt{7}}+\dfrac{2-\sqrt{2}}{\sqrt{2}-1}\)
\(=\sqrt{7}-\sqrt{2}+3-\sqrt{7}+\sqrt{2}\)
=3
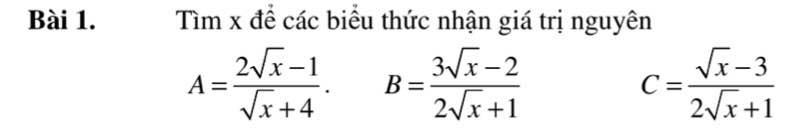

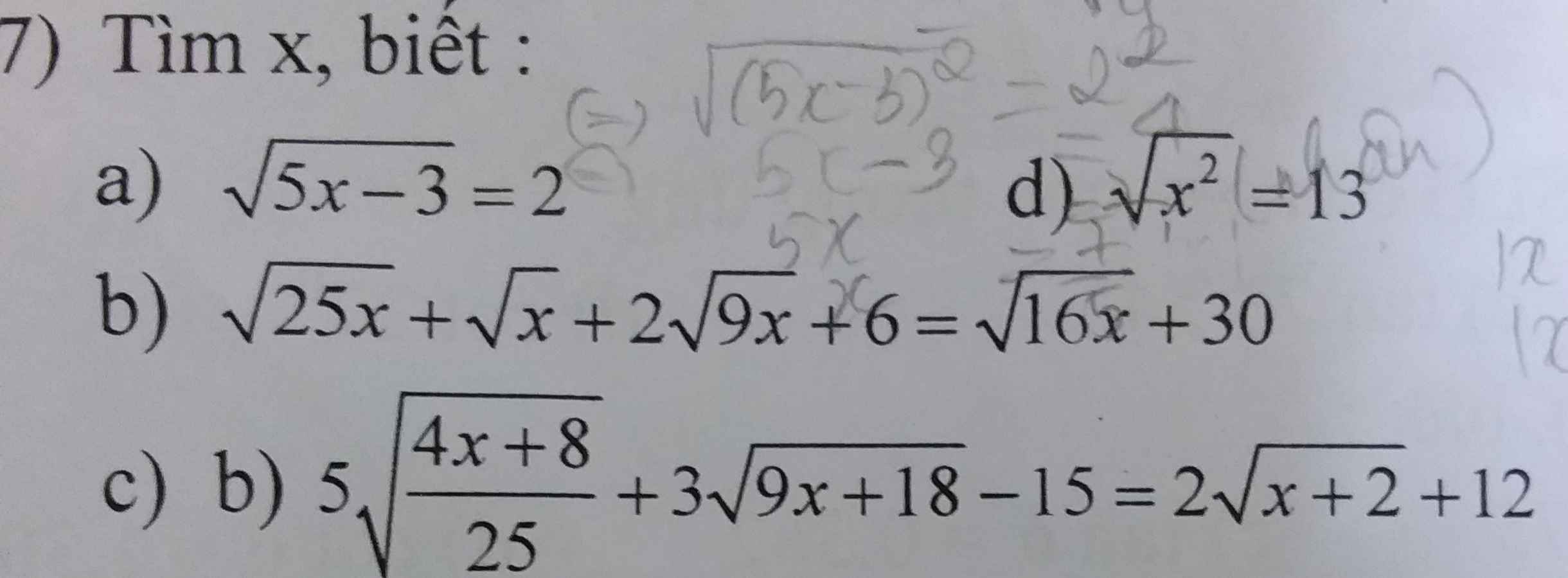




b) Để B nguyên thì \(3\sqrt{x}-2⋮2\sqrt{x}+1\)
\(\Leftrightarrow6\sqrt{x}-4⋮2\sqrt{x}+1\)
\(\Leftrightarrow-7⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}+1\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;-2;6;-8\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;3\right\}\)
hay \(x\in\left\{0;9\right\}\)
c) Để C nguyên thì \(\sqrt{x}-3⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}-6⋮2\sqrt{x}+1\)
\(\Leftrightarrow-7⋮2\sqrt{x}+1\)
\(\Leftrightarrow x\in\left\{0;9\right\}\)