Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay \(x=-4\) vào pt elip ta được:
\(\frac{y^2}{9}=1-\frac{16}{25}=\frac{9}{25}\Rightarrow\left[{}\begin{matrix}y=\frac{9}{5}\\y=-\frac{9}{5}\end{matrix}\right.\)
\(\Rightarrow MN=2.\frac{9}{5}=\frac{18}{5}\)

\(2c=F_1F_2=8\) \(\Rightarrow c=4\)
\(MF_1+MF_2+F_1F_2=18\Leftrightarrow2a+8=18\Rightarrow a=5\)
\(\Rightarrow e=\frac{c}{a}=\frac{4}{5}\)

Câu 1:
Đường tròn (C) tâm \(I\left(1;2\right)\) bán kính \(R=2\)
\(\overrightarrow{IM}=\left(2;2\right)=2\left(1;1\right)\)
Do AB luôn vuông góc AM nên đường thẳng AB nhận (1;1) là 1 vtpt
Phương trình AB có dạng: \(x+y+c=0\)
Theo công thức diện tích tam giác:
\(S_{IAB}=\frac{1}{2}IA.IB.sin\widehat{AIB}=\frac{1}{2}R^2sin\widehat{AIB}\le\frac{1}{2}R^2\)
\(\Rightarrow S_{max}=\frac{1}{2}R^2\) khi \(\widehat{AIB}=90^0\)
\(\Rightarrow d\left(I;AB\right)=\frac{R}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow\frac{\left|1+2+c\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\Leftrightarrow\left|c+3\right|=2\Rightarrow\left[{}\begin{matrix}c=-1\\c=-5\end{matrix}\right.\)
Có 2 đường thẳng AB thỏa mãn: \(\left[{}\begin{matrix}x+y-1=0\\x+y-5=0\end{matrix}\right.\)
TH1: \(x+y-1=0\Rightarrow y=1-x\)
Thay vào pt đường tròn: \(x^2+\left(1-x\right)^2-2x-4\left(1-x\right)+1=0\)
Giải ra tọa độ A hoặc B (1 cái là đủ) rồi tính được AM
TH2: tương tự.
Bạn tự làm nốt phần còn lại nhé
Đây là đề bài 1 chính thức nha bạn!
Trong Oxy, cho (C1): \(x^2+y^2-2x-4y+1=0\), M (3; 4)
a) Tìm tọa độ tâm I và tính bán kính R của (C1).
b) Viết phương trình tiếp tuyến d1 với đường tròn (C1) tại giao điểm của\(\Delta_1:x-2y+5=0,\Delta_2:3x+y+1=0\)
c) Viết phương trình tiếp tuyến d2 với đường tròn (C1) biết d2 song song với d: \(4x+3y+2020=0\)
d) Viết phương trình đường tròn (C2) có tâm M, cắt đường tròn (C1) tại hai điểm A, B sao cho \(S_{\Delta IAB}\)lớn nhất.

Câu 1:
Phương trình hoành độ giao điểm của (P) và (d):
\(x^2-4x=-x-2\)
⇔ \(x^2-3x+2=0\)
⇔ \(\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
Với x= 2 ⇒ y=-2 -2 = -4
Với x= 1 ⇒ y = -1 -2 = -3
Vậy chọn B: M( 1; -3) và N(2;-4)
Câu 2:
Vì (d) tiếp xúc với (P)
nên Δ = 0 ⇒ phương trình có một nghiệm kép
Vậy chọn D: y= -x +1
Câu 3:
(P) : y =\(x^2+4x+4\)
Để (P) có điểm chung với trục hoành ⇔ y =0
Vậy chọn B : 1
Câu 4:
Phương trình hoành độ giao điểm của hai parabol:
\(x^2-4=14-x^2\)
⇔ \(2x^2-18=0\)
⇔\(\left[{}\begin{matrix}x=3\Rightarrow y=14-3^2=5\\x=-3\Rightarrow y=14-\left(-3\right)^2=5\end{matrix}\right.\)
Vậy chọn C : (3;5) và (-3;5)
Câu 5: (P) : y= \(x^2-2x+m-1\)
Để (P) không cắt Ox
⇔ Δ < 0
⇔ \(b^2-4ac< 0\)
⇔ \(\left(-2\right)^2-4\left(m-1\right)< 0\)
⇔ 4 - 4m +4 < 0
⇔ -4m < -8
⇔ m > 2
Vậy chọn B : m> 2

Bài 1:
\(9x^2+25y^2=225\Leftrightarrow\frac{x^2}{25}+\frac{y^2}{9}=1\)
\(\Rightarrow c^2=a^2-b^2=25-9=16\Rightarrow c=4\Rightarrow F_2\left(4;0\right)\)
Đường thẳng qua \(F_2\) vuông góc trục lớn có pt \(x=4\)
\(\Rightarrow9.4^2+25y^2=225\Leftrightarrow25y^2=81\Rightarrow\left[{}\begin{matrix}y=\frac{9}{5}\\y=-\frac{9}{5}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}M\left(4;\frac{9}{5}\right)\\N\left(4;-\frac{9}{5}\right)\end{matrix}\right.\)
Bài 2:
Gọi pt elip có dạng \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{1}{a^2}+\frac{3}{4b^2}=1\\\frac{0}{a^2}+\frac{1}{b^2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b^2=1\\a^2=4\end{matrix}\right.\)
Phương trình elip: \(\frac{x^2}{4}+\frac{y^2}{1}=1\)

Lời giải:
Đường tròn (C):
\(x^2+y^2+2x-2y-2=0\)
\(\Leftrightarrow (x+1)^2+(y-1)^2=4=2^2\)
Do đó đường tròn (C) là đường tròn có tâm \(I(-1;1)\) bán kính \(R=2\)
Từ $I$ kẻ \(IH\perp BC\) thì $H$ là trung điểm của $BC$
\(\Rightarrow BH=\sqrt{3}\)
Áp dụng định lý Pitago:
\(IH=\sqrt{BI^2-BH^2}=\sqrt{R^2-3}=\sqrt{4-3}=1(1)\)
Mà: \(IH=d(I, d)=\frac{|-1-m+2m+3|}{\sqrt{m^2+1}}=\frac{|m+2|}{\sqrt{m^2+1}}(2)\)
Từ \((1); (2)\Rightarrow \frac{|m+2|}{\sqrt{m^2+1}}=1\)
\(\Rightarrow (m+2)^2=m^2+1\Leftrightarrow m^2+4m+4=m^2+1\)
\(\Leftrightarrow 4m+3=0\Leftrightarrow m=\frac{-3}{4}\)



Dể thấy d: x+4= 0 là đường thẳng đi qua tiêu điểm F1( -4;0) của (E) .
Do đó .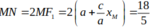
Chọn C.