Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
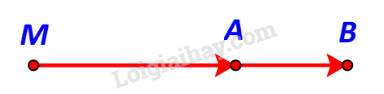
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
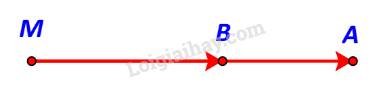
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

bẹn tự vẽ hình nhé! Gọi I và J lần lượt là trung điểm của AD và BC.
Theo giả thiết: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{O}a\)
\(\Leftrightarrow2\left(\overrightarrow{OI}+\overrightarrow{OJ}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\)O,I, J thẳng hàng.(1)
\(\Delta OAD\)cân tại \(O\Rightarrow OI\perp AB\)(2)
\(\Delta OBC\)cân tại \(O\Rightarrow OJ\perp BC\)(3)
Từ 1,2,3 => AD//BC
Tương tự ta chứng minh được AB//CD
Vậy tứ giáo ABCD nội tiếp được trong đường tròn, nên tứ giác ABCD là hình chữ nhật. (đpcm)
Thanks Đặng Ngọc Quỳnh
P/s:trc chỗ (2) hình như là OI vuông góc với AD mới đúng :P

Xét ΔOAI và ΔOBI có
OA=OB
OI chung
AI=BI
Do đó: ΔOAI=ΔOBI
Suy ra: \(\widehat{AOI}=\widehat{BOI}\)
hay OI là tia phân giác của góc xOy

a) Giả sử véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) .
Dựng hình bình hành OABD.
O A B D
Theo quy tắc hình bình hành: \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\).
Theo giả thiết thì OD là tia phân giác góc \(\widehat{AOB}\).
Vì vậy hình bình hành OABD là hình thoi.
Suy ra OA = OB.
- Giả sử OA = OB.
Khi đó hình bình hành OABD có OA = OB nên tứ giác OABD là hình thoi.
Kết luận: Điều kiện cần và đủ để véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) là OA = OB.

 | = |
| = | |.cos(
|.cos( ,
, 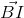 .
.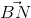 =
= 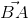 lý luận tương tự.
lý luận tương tự.
Hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau \( \Leftrightarrow \) hai tia OA, OB đối nhau và OA = OB.
\( \Leftrightarrow \) O là trung điểm của AB hay AB là đường kính của đường tròn (O).
Vậy điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau là AB là đường kính của đường tròn (O).