1. Cho tam giác ABC có ba góc nhọn. Đường tròn tâm (O) đường kính BC cắt hai cạnh Ab , AC lần lượt tại E và F. Gọi H là giao điểm của CE và BF, D là giao điểm của AD và BC.a) Chứng minh AEHF nội tiếpb) Chứng minh EC là tia phân giác của góc DEFc) Đường thẳng EF cắt BC tại M, Chứng minh MB.MC=ME.MF=MO.MDd) AD cắt đường tròn (O) tại I, chứng minh MI là tiếp tuyến của (O) e) Đường thẳng qua D song...
Đọc tiếp
1. Cho tam giác ABC có ba góc nhọn. Đường tròn tâm (O) đường kính BC cắt hai cạnh Ab , AC lần lượt tại E và F. Gọi H là giao điểm của CE và BF, D là giao điểm của AD và BC.
a) Chứng minh AEHF nội tiếp
b) Chứng minh EC là tia phân giác của góc DEF
c) Đường thẳng EF cắt BC tại M, Chứng minh MB.MC=ME.MF=MO.MD
d) AD cắt đường tròn (O) tại I, chứng minh MI là tiếp tuyến của (O)
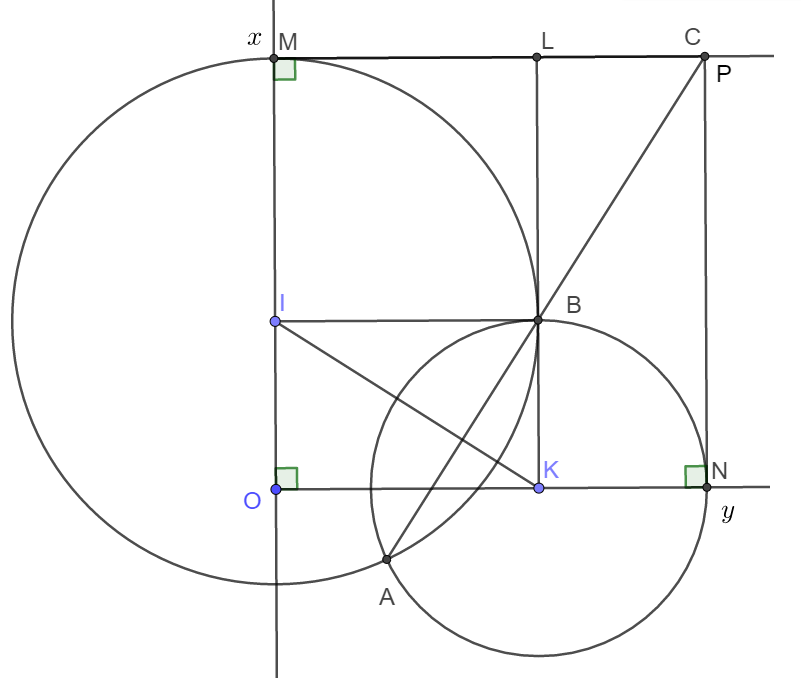
e) Đường thẳng qua D song song với MF, cắt AB và AC lần lượt tại K và L. Chứng minh : M, K, L, O cùng thuộc một đường tròn.
2. Cho điểm A nằm ngoài đường tròn (O;R), từ A kẻ hai tiếp tuyến AB, AC và cát tuyến ADE (B, C là hai tiếp điểm, O nằm trong góc BAE). BC cắt OA tại I
a) Chứng minh: tứ giác ABOC nội tiếp và OA vuông góc với BC
b) Chứng minh OI.IA=(BC^2)/4 và AB.AC = AD.AE
c) Vẽ đường kính BK của (O), Tia KD cắt OA tại F. Chứng minh FB vuông góc với EB
d) Gọi H là trung điểm của DE, từ B kẻ dây BN song song với DE. Chứng minh 3 điểm N, H, C thẳng hàng.
3. Từ một điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB và AC đến (O) (B và C là các tiếp điểm) và một cát tuyến ADE không đi qua tâm O (D nằm giữa A và E), gọi I là trung điểm của DE.
a) Chứng minh 5 điểm A;B;O;I;C cùng nằm trên một đường tròn suy ra IA là phân giác của góc BIC
b) BC cắt AE tại K. Chứng minh KA.KI=KD.KE
c) Qua C kẻ đường thẳng song với AB, đường này cắt các đướng thẳng BE, BD lần lượt tại P và Q. Chứng minh C là trung điểm của PQ.
d) Đường thẳng OI cắt đường tròn (O) tại S và H. Đường thẳng HK cắt (O) tại điểm thứ hai là T. Chứng minh 3 điểm A, T, S thẳng hàng
Giúp em giai cau 1 d, cau 2 c, câu 3 c , cảm ơn nhiều




A B D E K O C d1 d2 H I G
a/
\(d_1;d_2\) là tiếp tuyến với đường tròn tại A và B \(\Rightarrow d_1\perp AB;d_2\perp AB\) => \(d_1\)//\(d_2\)
Xét tg vuông ABK có
\(\widehat{ACB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AK^2=KC.KB\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
b/
Ta có
DA=DC (2 tiếp tuyến của 1 đường tròn cùng xuất phát từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau) (1)
EC=EB (lý do như trên) => tg EBC cân tại E\(\Rightarrow\widehat{ECB}=\widehat{KBE}\) (2 góc ở đáy của tg cân) (*)
\(\widehat{KBE}=\widehat{AKB}\) (góc so le trong) (**)
\(\widehat{KCD}=\widehat{ECB}\) (Góc đối đỉnh) (***)
Từ (*) (**) và (***) \(\Rightarrow\widehat{AKB}=\widehat{KCD}\) => tg DCK cân tại D => DC=DK (2)
Từ (1) và (2) => DA=DK nên K là trung điểm của AK
c/ Gọi I là giao của CH với BD
Ta có
\(CH\perp AB;d_1\perp AB\) => CH//\(d_1\)
\(\Rightarrow\frac{IC}{DK}=\frac{BC}{BK}=\frac{BH}{BA}=\frac{IH}{DA}\) (Talet trong tam giác)
Mà DK=DA => IC=IH => BD đi qua trung điểm I của CH
d/
câu a ý số 2 bạn còn cách nào khác ko? Tại mk chx hc góc nội tiếp chắn nửa đường tròn