Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

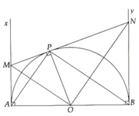
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

Bài 5:
a: Xét tứ giác BHCA có \(\widehat{BHA}=\widehat{BCA}=90^0\)
nên BHCA là tứ giác nội tiếp
=>B,H,C,A cùng thuộc một đường tròn
b: Xét ΔKHA vuông tại H và ΔKCB vuông tại C có
\(\widehat{HKA}\) chung
Do đó: ΔKHA đồng dạng với ΔKCB
=>\(\dfrac{KH}{KC}=\dfrac{KA}{KB}\)
=>\(KH\cdot KB=KA\cdot KC\)
c: Gọi giao điểm của KE với BA là M
Xét ΔKBA có
AH,BC là các đường cao
AH cắt BC tại E
Do đó: E là trực tâm của ΔKBA
=>KE\(\perp\)BA tại M
Xét ΔBME vuông tại M và ΔBCA vuông tại C có
\(\widehat{MBE}\) chung
Do đó: ΔBME đồng dạng với ΔBCA
=>\(\dfrac{BM}{BC}=\dfrac{BE}{BA}\)
=>\(BM\cdot BA=BC\cdot BE\)
Xét ΔAME vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAE}\) chung
Do đó: ΔAME đồng dạng với ΔAHB
=>\(\dfrac{AM}{HA}=\dfrac{AE}{AB}\)
=>\(AH\cdot AE=AM\cdot AB\)
\(BC\cdot BE+AH\cdot AE=BM\cdot BA+AM\cdot AB=AB^2\) không đổi

a) x4+x3+2x2+x+1=(x4+x3+x2
)+(x2+x+1)=x2
(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3
-3abc=a3+3ab(a+b)+b3+c3
-(3ab(a+b)+3abc)=(a+b)3+c3
-3ab(a+b+c)
=(a+b+c)((a+b)2
-(a+b)c+c2
)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2
-ac-ab+c2
-3ab)=(a+b+c)(a2+b2+c2
-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2
(y-z)+y2
(z-x)+z2
(x-y)=x2
(y-z)-y2
((y-z)+(x-y))+z2
(x-y)
=x2
(y-z)-y2
(y-z)-y2
(x-y)+z2
(x-y)=(y-z)(x2
-y2
)-(x-y)(y2
-z2
)=(y-z)(x2
-2y2+xy+xz+yz)
k mk nha $_$
:D
x y M N A O B 1 2 3 4
a) Vì MA , MI là 2tt của đường tròn (O) , nên ^O1 = ^O2 (1)
Vì NB , NI là 2tt của nửa đường tròn (O) , nên ^O3 = ^O4 (2)
Từ (1) và (2) => \(\widehat{O_2}+\widehat{O_3}=\widehat{O_1}+\widehat{O_4}=\frac{180^o}{2}=90^o\)
Mà ^MON = 90^o
Vậy : ^MON = 90^o
b) Theo t/c 2tt cắt nhau , ta có :
AM = MI ; NI = NB
MN = MI + IN = AM + BN
Vậy : MN = AM + BN ( đpcm )
c) Áp dụng hệ thức lượng tam giác trong tam giác OMN vuông tại O , đường cao OI
Ta có : \(OI^2=IM.IN\)
\(\Rightarrow IM.IN=R^2\)( R bán kính )
Mặt khác : MA = MI ; NB = NT
Vậy : AM . BN = R^2 ( đpcm )

a: Xét (O) có
CA,CM là tiếp tuyến
nênCA=CM và OC là phân giác của góc AOM(1)
mà OA=OM
nên OC là trung trực của AM
=>OC vuông góc với AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Xét (O)có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>MB vuông góc MA
=>MB//OC
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
=>OC vuông góc với OD
mà OM vuông góc DC
nên MC*MD=OM^2
=>AC*BD=R^2
c: Gọi H là trung điểm của CD
Xét hình thang ABDC có
H,O lần lượtlà trung điểm của CD,AB
nên HO là đường trung bình
=>HO//AC//BD
=>HO vuông góc với AB
=>AB là tiếp tuyến của (H)

* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
a) Xét (O) có
NA là tiếp tuyến có A là tiếp điểm(gt)
NE là tiếp tuyến có E là tiếp điểm(gt)
Do đó: ON là tia phân giác của \(\widehat{AOE}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{AOE}=2\cdot\widehat{EON}\)
Xét (O) có
ME là tiếp tuyến có E là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OM là tia phân giác của \(\widehat{EOB}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{EOB}=2\cdot\widehat{EOM}\)
Ta có: \(\widehat{EOA}+\widehat{EOB}=180^0\)(hai góc kề bù)
hay \(2\cdot\widehat{EON}+2\cdot\widehat{EOM}=180^0\)
\(\Leftrightarrow\widehat{EON}+\widehat{EOM}=90^0\)
hay \(\widehat{MON}=90^0\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào \(\Delta\)ONM vuông tại O có OE là đường cao ứng với cạnh huyền NM, ta được:
\(ME\cdot NE=OE^2\)
mà OE=R
nên \(ME\cdot NE=R^2\)(đpcm)