Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình.
a) CD vuông góc AB => CH = DH = 6. Ta có: HA.HB = CH2 \(\Rightarrow HA\left(13-HA\right)=36\Leftrightarrow HA^2-13HA+36=0\)
\(\Leftrightarrow\left(HA-9\right)\left(HA-4\right)=0\Leftrightarrow\)HA = 9 hoặc HA = 4 => HB = 4 hoặc HB = 9

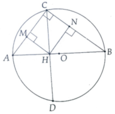
a, Tính được HA=4cm; HB=9cm
b, Tính được HA=4cm; HB=9cm
c, Tính được HM = 12 13 13 cm, HN = 18 13 13 cm
Từ đó tính được S C M H N = 216 13 c m 2

b/ Gọi G là giao điểm của AB và DF
Ta có :
Góc ACQ = góc AHQ ( t/g ACHQ n.t )
Góc ACQ = góc ADF ( 2 góc n.t chắn cung AF )
=> Góc AHQ = góc ADF
Mà 2 góc ở vị trí đồng vị
Nên \(HQ//DF\)
Mặc khác \(HQ\perp AB\)tại Q
=> \(DF\perp AB\)tại G
Xét tứ giác GBNF ta có:\(B\widehat{G}F+B\widehat{N}F=180^0\)
=> Tứ giác GBNF nội tiếp =>\(N\widehat{G}F=N\widehat{B}F\)
Mà \(N\widehat{B}F=C\widehat{A}F\)( tứ giác ACBF n.t (O))
Nên \(N\widehat{G}F=C\widehat{A}F\left(1\right)\)
Xét tứ giác GMAF ta có: \(A\widehat{M}F=A\widehat{G}F\left(=90^0\right)\)
=> Tứ giác GMAF n.t =>\(M\widehat{A}F+M\widehat{G}F=180^0\left(2\right)\)
(1) và (2) => \(N\widehat{G}F+M\widehat{G}F=180^0\)
=> \(\overline{M,G,N}\)
Mà G là giao điểm của AB và DF
Nên MN,AB,DF đồng quy tại G
MN là đường thẳng simson nha bạn

tích cho t đi
i love you....
Bạn lê duy mạnh, t tặng bạn 1 cái dis này