Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5

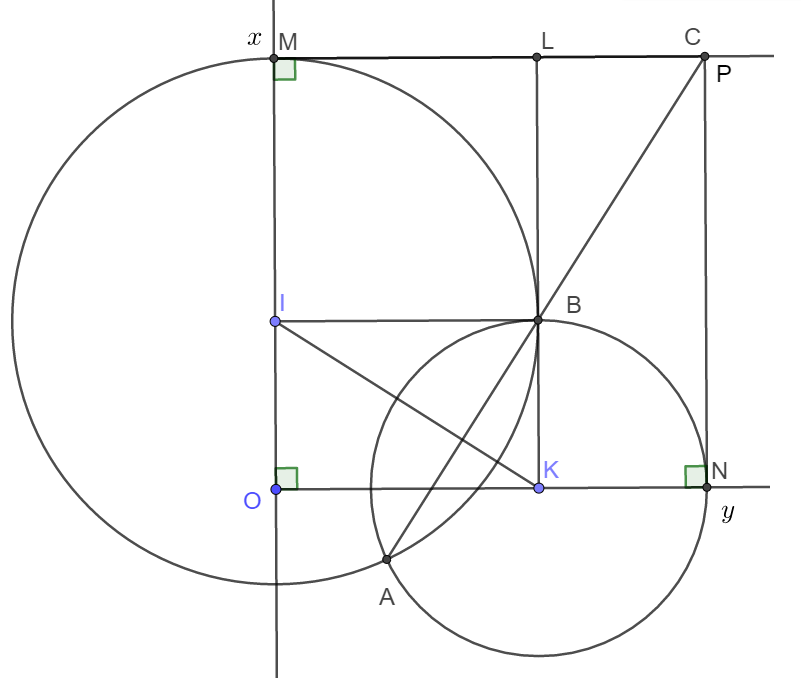
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.

Giải
a) Ta có: OM⊥JM (JM là tiếp tuyến của (O))
NK⊥JM (K là trực tâm của ΔJMN)
⇒ OM // NK
Chứng minh tương tự được ON // MK
⇒ OMKN là hình bình hành
Hình bình hành OMKN có hai đường chéo OK và MN cắt nhau tại H
=⇒ H là trung điểm của OK.
b) Hình bình hành OMKN có OM = ON = a nên là hình thoi
⇒ OM = MK ⇒ΔOMK cân tại M
ΔOMJ vuông tại M, có:
có \(\widehat{MOJ}=\frac{OM}{OJ}=\frac{a}{2a}=\frac{1}{2}\Rightarrow\widehat{MOJ}=60^0\)
⇒ΔOMK là tam giác đều
⇒OK = OM = a ⇒K ∈ (O ; a)
c) ΔOMH vuông tại H
⇒MH = OM . sin\(\widehat{MOH}\)=a . sin\(60^0=\frac{a\sqrt{3}}{2}\)hay \(\frac{a\sqrt{3}}{2}\)
Hok Tốt !
# mui #
Chú Thích : Mk có gửi ảnh nếu bn ko thấy thì vào thống kê hỏi đáp của mk nha