Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn

a) \(\Delta ABE\)nội tiếp đường tròn đường kính \(AB\)
\(\Rightarrow\)\(\Delta ABE\perp E\)
\(\Rightarrow\)\(AEB\lambda=90\)độ
Tứ giác\(BEFI\)nội tiếp đường tròn đường kính \(FB\)

OB=OC
MB=MC
=>OM là trung trực của BC
=>OM vuông góc BC tại I
góc CHO+góc CIO=180 độ
=>CHOI nội tiếp

Hình bạn tự vẽ nhé :
Xét \(\Delta\)OAB có : OA=OB=R \(\Rightarrow\Delta\)OAB cân tại O ⇒ OM là đường trung tuyến đồng thời là đường phân giác ⇒ góc MOA= góc MOB ⇒ góc EOA= góc EOB Lại có góc EOA = số đo cung EA; góc EOB = số đo cung EB ⇒ số đo cung EA = số đo cung EB \(\Rightarrow\) E là điểm chính giữa của cung AB

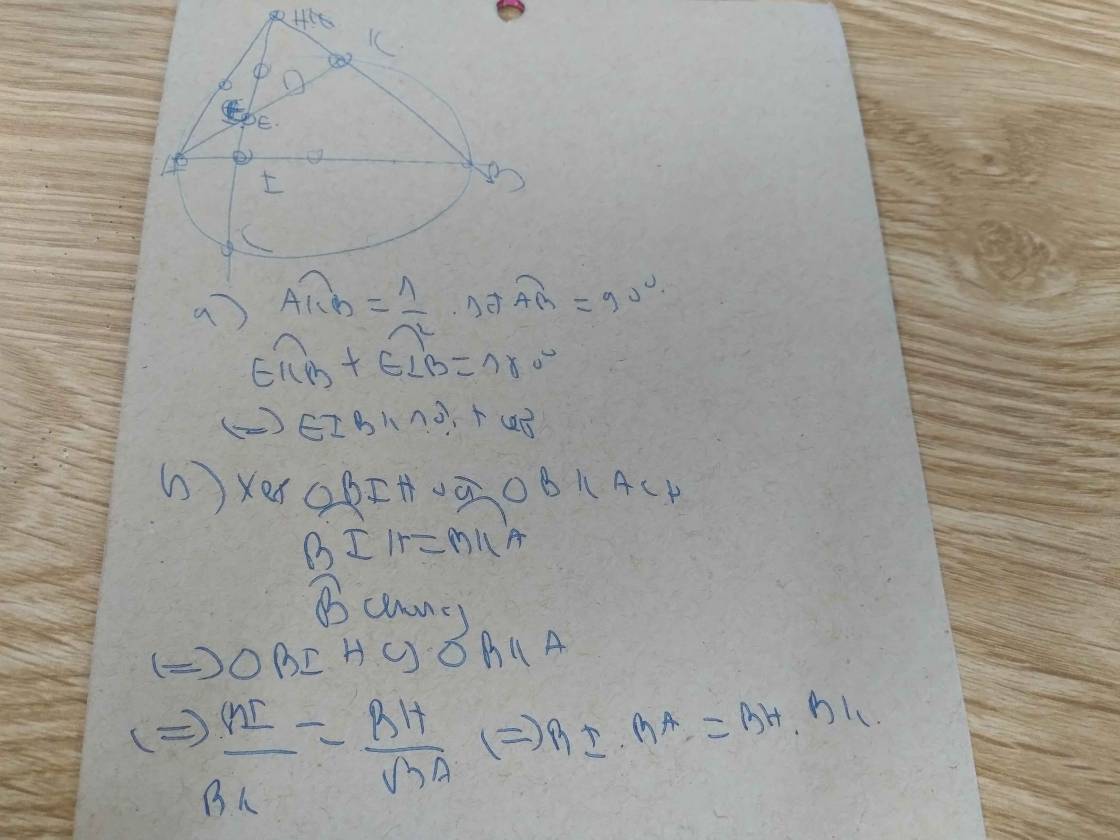
Lời giải:$I$ chính giữa cung $AB$ nên $IA=IB$
Lại có $OA=OB=R$
Do đó $OI$ là đường trung trực của $AB$
$\Rightarrow IO\perp AB$ tại $H$ hay $IH\perp AB$
Tam giác $IAB$ cân tại $I$ nên đường cao $IH$ đồng thời là đường trung tuyến $\Rightarrow H$ là trung điểm $AB$
Do đó $AH=HB$ (đpcm)
Hình vẽ: