Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

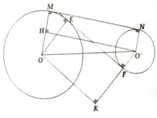
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

a: Xét (O) có
AT là tiếp tuyến
AT' là tiếp tuyến
Do đó: AT=AT'
hay A nằm trên đường trung trực của TT'(1)
Ta có: OT=OT'
nên O nằm trên đường trung trực của TT'(2)
Từ (1) và (2) suy ra AO là đường trung trực của TT'
Xét ΔOTA vuông tại T có TI là đường cao
nên \(AT^2=AI\cdot AO\)
b: Xét ΔAIJ vuông tại I và ΔAHO vuông tại H có
\(\widehat{HAO}\) chung
Do đó: ΔAIJ\(\sim\)ΔAHO