Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O;R) có:
\(\widehat{BCD}\)là góc nt chắn cung BC
\(\widehat{BAC}\)là góc nt chắn cung BC
\(\Rightarrow\widehat{BCD}=\widehat{BAC}=sđ\widebat{BC}\)
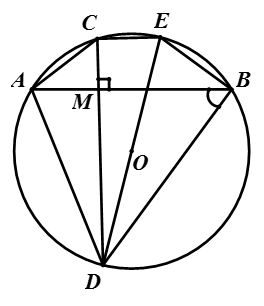
Vì dây \(AB\perp CD\)tại M nên \(\widehat{M}=90^o\)
Xét \(\Delta ACM\)và \(\Delta DBM\):
\(\hept{\begin{cases}\widehat{AMC}=\widehat{DMB}=90^o\\\widehat{BAC}=\widehat{BCD}\end{cases}}\)
\(\Rightarrow\Delta ACM\infty\Delta DBM\left(gg\right)\)
\(\Rightarrow\frac{AM}{DM}=\frac{MC}{MB}\Rightarrow AM.MB=MC.DM\)
b) Vì \(\Delta ACM\infty DBM\Rightarrow\widehat{ACM}=\widehat{DBM}\)
Xét \(\left(O;R\right):\)
\(\Delta CDE\)nt (O), cạnh DE là đường kính\(\Rightarrow\Delta CDE\)vuông tại C\(\Rightarrow CD\perp CE\Rightarrow\widehat{DCE}=90^o\)
\(\Delta BDE\)nt \(\left(O\right),\)cạnh DE là đường kính\(\Rightarrow\Delta BDE\)vuông tại B\(\Rightarrow\widehat{DBE}=90^o\)
Có\(\widehat{MAC}+\widehat{ACM}=90^o\Rightarrow\widehat{MAC}=90^o-\widehat{ACM}\)
Và \(\widehat{ABE}+\widehat{DBM}=90^o\Rightarrow\widehat{ABE}=90^o-\widehat{DBM}\)
Mà \(\widehat{ACM}=\widehat{DBM}\)\(\Rightarrow\widehat{MAC}=\widehat{ABE}\)
Do \(AB\perp CD,CD\perp CE\Rightarrow AB//CE\)
Xét tg ABCE có:
\(AB//CE\)
\(\widehat{MAC}=\widehat{ABE}\)
\(\Rightarrow Tg\)ABCE là hthang cân
c) Áp dụng đ/lí Pi-ta-go lần lượt vào các \(\Delta AMC,\Delta BCM;\Delta BDM;\Delta ADM;\Delta BDE\)có:
\(AM^2=AC^2-CM^2\)(1)
\(MB^2=BC^2-CM^2\)(2)
\(MC^2=BC^2-BM^2\)(3)
\(MD^2=BD^2-BM^2\)(4)
\(DE^2=BD^2+BE^2\)(5)
Công từng vế của (1)(2)(3)(4) ta đc đẳng thức:
\(MA^2+MB^2+MC^2+MD^2=AC^2-CM^2+BC^2-CM^2+BC^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BC^2-2CM^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BM^2-BM^2+BD^2-BM^2\)(vì \(BM^2=BC^2-CM^2\))
\(=AC^2+BD^2\)
\(=BE^2+BD^2\)(vì AC=BE do ABCE là hthang cân)
\(=DE^2\)(c/m (5))
Mà DE là đường kính của (O) nên DE=2R\(\Rightarrow DE^2=\left(2R\right)^2=4R^2\)
Vậy \(MA^2+MB^2+MC^2+MD^2\)có g/trị ko đổi khi M thay đổi trong (O)

\(MA.MB=MC.MD\Leftrightarrow\Delta MAC\approx\Delta MDB\left(G-G\right)\)
Duong thang OM cat duong tron tai E,F
chung minh tuong tu ta co \(MA.MB=ME.MF=\left(R-d\right)\left(R+d\right)=R^2-d^2\)

A B C D M E O
Gọi E là điểm đối xứng với C qua tâm O của đường tròn
Dễ dàng chứng minh được ABED là hình thang cân.
=> BD = AE
Ta có : \(MA^2+MB^2+MC^2+MD^2=\left(MA^2+MC^2\right)+\left(MB^2+MD^2\right)=AC^2+BD^2\)
\(=AC^2+AE^2=CE^2=\left(2R\right)^2=4R^2\) KHÔNG ĐỔI.

a) Xét ΔAMC và ΔDMB có:
góc ACD = góc ABD (góc nội tiếp cùng chắn cung AD)
góc AMC = góc BMD = 90o (gt)
=> ΔAMC ∼ ΔDMB (g.g)
=> MA/MD = MC/MB => MA.MB = MC.MD
b) Vì góc DCE = 90 độ (góc nội tiếp chắn nửa đường tròn)
=> CD ⊥ CE
Mà CD ⊥ AB (gt)
=> AB // CE
=> Tứ giác ABEC là hình thang (1).
Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE nên \(\stackrel\frown{AC}=\stackrel\frown{BE}\)
=> \(sd\stackrel\frown{AE}+sd\stackrel\frown{EC}=sd\stackrel\frown{BC}+sd\stackrel\frown{EC}\)
=>\(sd\stackrel\frown{AE}=sd\stackrel\frown{BC}\) => \(\widehat{ABE}=\widehat{CAB}\) (2)
Từ (1) và (2) => đpcm
c, Vì \(\stackrel\frown{AC}=\stackrel\frown{BE}\Rightarrow AC=BE\)
Ta có: góc DAE = 90 độ (góc nội tiếp chắn nửa đường tròn)
Ta có: \(MA^2+MB^2+MC^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)\) (áp dụng pytago vào t/g MAD và MBC)
\(=AD^2+BC^2=AD^2+AE^2=DE^2=4R^2\) không đổi (pytago)