Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

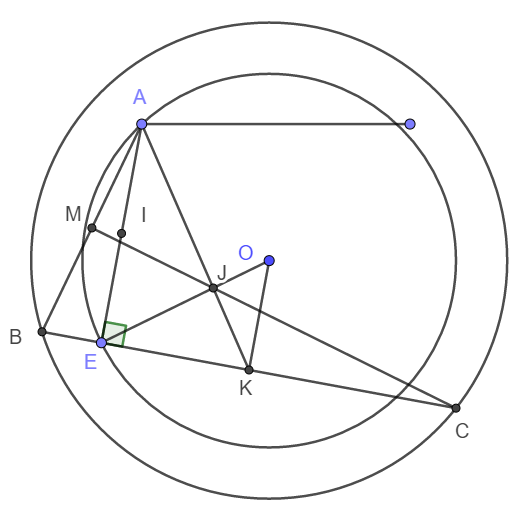
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.


( 1 số phần cơ bản sẽ làm tắt nha, cái đấy bạn sẽ tự trình bày rõ nhá, nhất là chứng minh tứ giác nội tiếp sẽ rút ngắn lại )
a)\(\widehat{ABO}=\widehat{AEO}=90^0\)
\(\Rightarrow ABEO\)nội tiếp
=> A,B,E,O thuộc 1 đường tròn
b) Xét tam giác AMC và tam giác ACN có:
\(\hept{\begin{cases}\widehat{NAC}chung\\\widehat{ACM}=\widehat{ANC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\end{cases}\Rightarrow\Delta AMC~\Delta ACN\left(g-g\right)}\)
\(\Rightarrow\frac{AM}{AC}=\frac{AC}{AN}\)
\(\Rightarrow AC^2=AM.AN\)
c) \(\widehat{MJC}+\widehat{MFC}=180^0\)
\(\Rightarrow MJCF\)nội tiếp
\(\Rightarrow\widehat{MFJ}=\widehat{MCJ}\)
Mà \(\widehat{MCJ}=\widehat{MBC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\)
\(\Rightarrow\widehat{MFJ}=\widehat{MBC}\left(1\right)\)
CMTT \(\widehat{MFI}=\widehat{MCB}\left(2\right)\)
Xét tam giác MBC có: \(\widehat{CMB}+\widehat{MCB}+\widehat{MBC}=180^0\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow\widehat{CMB}+\widehat{MFJ}+\widehat{MFI}=180^0\)
\(\Rightarrow\widehat{CMB}+\widehat{PFQ}=180^0\)
\(\Rightarrow MPFQ\)nội tiếp
\(\Rightarrow\widehat{MPQ}=\widehat{MFQ}\)mà \(\widehat{MFQ}=\widehat{MBC}\left(cmt\right)\)
\(\Rightarrow\widehat{MPQ}=\widehat{MBC}\)mà 2 góc này ở vị trí đồng vị
\(\Rightarrow PQ//BC\)
d) Xét tam giác MIF và tam giác MFJ có:
\(\hept{\begin{cases}\widehat{MIF}=\widehat{MFJ}\left(=\widehat{MBF}\right)\\\widehat{MJF}=\widehat{MFI}\left(=\widehat{MCF}\right)\end{cases}\Rightarrow\Delta MIF~\Delta MFJ\left(g-g\right)}\)
\(\Rightarrow\frac{MI}{MF}=\frac{MF}{MJ}\)
\(\Rightarrow MI.MJ=MF^2\)
MI.MJ lớn nhất \(\Leftrightarrow MF^2\)lớn nhất
Mà \(MF=\frac{1}{2}MN\)
\(\Rightarrow MF^2=\frac{1}{4}MN^2\)
\(\Rightarrow MF\)lớn nhất <=> MN lớn nhất \(\Leftrightarrow MN\)là đường kính (O)
\(\Leftrightarrow M\)là điểm chính giữa cung BC
Vậy MI.MJ lớn nhất <=> M là điểm chính giữa cung BC.
( KO hiểu thì hỏi mình nha )

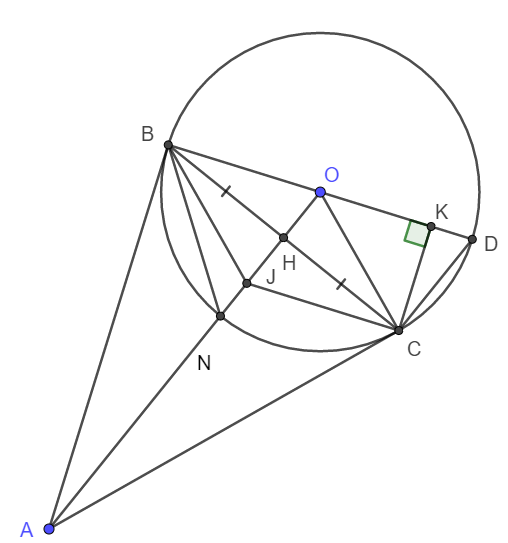
a) Tam giác vuông ABO và ACO có chung cạnh huyền AO nên O, B, A, C cùng thuộc đường tròn đường kính AO.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC là tam giác cân tại A.
Lại có AO là phân giác nên đồng thời là đường trung tuyến. Vậy thì AO đi qua H hay A, H, O thảng hàng.
Theo liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung, ta có \(\widehat{KDC}=\frac{\widehat{BOC}}{2}\)
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có: \(\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Suy ra \(\widehat{KDC}=\widehat{COA}\)
Vậy thì \(\Delta KDC\sim\Delta COA\left(g-g\right)\Rightarrow\frac{CK}{AC}=\frac{CD}{AO}\Rightarrow AC.CD=CK.AO\)
c) Ta thấy \(\widehat{ABN}=\widehat{NBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung chắn các cung bằng nhau)
Vậy nên BN là phân giác góc ABC.
Lại có AN là phân giác góc BAC nên N là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi J là trực tâm tam giác ABC. Ta có ngay \(JC\perp AB;BJ\perp AC\)
Vậy thì BO // JC ; BJ // OC
Suy ra tứ giác JBOC là hình bình hành.
Lại có OB = OC nên JBOC là hình thoi.
Từ đó ta có JB = JC = OB = OC = R.
Vậy khi A di chuyển trên tia By cố định thì BJ = R hay J thuộc đường tròn tâm B, bán kính R.
