Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK⊥CD tại K
ΔOEF cân tại O
mà OL là đường trung tuyến
nên OL⊥EF
mà EF//CD
nên OL⊥CD
Ta có: OK⊥CD
OL⊥CD
mà OK,OL có điểm chung là O
nên K,O,L thẳng hàng
b: Ta có: \(OM=MA=\frac{OA}{2}\)
\(ON=NB=\frac{OB}{2}\)
mà OA=OB
nên OM=MA=ON=NB
OM=ON nên O là trung điểm của MN
Xét ΔOKM vuông tại K và ΔOLN vuông tại L có
OM=ON
\(\hat{KOM}=\hat{LON}\) (hai góc đối đỉnh)
Do đó: ΔOKM=ΔOLN
=>OK=OL
mà OK=d(O;CD) và OL=d(O;EF)
nên CD=EF
=>CK=KD=EL=LF
Xét tứ giác CLFK có
CK//LF
CK=LF
Do đó: CLFK là hình bình hành
=>CF cắt LK tại trung điểm của mỗi đường
mà O là trung điểm của LK
nên O là trung điểm của CF
=>CF là đường kính của (O)(2)
Xét tứ giác ELDK có
EL//DK
EL=DK
Do đó: ELDK là hình bình hành
=>ED cắt LK tại trung điểm của mỗi đường
mà O là trung điểm của LK
nên O là trung điểm của ED
=>ED là đường kính của (O)(1)
Từ (1),(2) suy ra ED=CF
Xét tứ giác EFDC có
EF//DC
EF=DC
Do đó: EFDC là hình bình hành
Hình bình hành EFDC có ED=FC
nên EFDC là hình chữ nhật
Đề bài:
Cho đường tròn \(\left(\right. O , R \left.\right)\) với đường kính \(A B\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(O A\), \(O B\). Qua \(M\), \(N\) lần lượt kẻ các dây \(C D\), \(E F\) song song với nhau (với \(C\), \(E\) cùng thuộc nửa đường tròn đường kính \(A B\)). Gọi \(K\), \(L\) lần lượt là trung điểm của \(C D\), \(E F\).
Chứng minh các câu sau:
a) \(O\), \(K\), \(L\) thẳng hàng.
b) \(C D F E\) là hình chữ nhật.
c) Giả sử các dây \(C D\) và \(E F\) cùng tạo với \(A B\) một góc 30 độ. Tính diện tích hình chữ nhật \(C D F E\) theo \(R\).
Giải phần (a): Chứng minh \(O\), \(K\), \(L\) thẳng hàng
Cách tiếp cận:
- Trung điểm và tính chất đối xứng:
- Vì \(M\) và \(N\) là trung điểm của \(O A\) và \(O B\), ta có:
\(\overset{\rightarrow}{O M} = \frac{1}{2} \overset{\rightarrow}{O A} , \overset{\rightarrow}{O N} = \frac{1}{2} \overset{\rightarrow}{O B}\) - Các dây \(C D\) và \(E F\) lần lượt kẻ qua \(M\) và \(N\) song song, nghĩa là các vectơ chỉ phương của chúng sẽ song song.
- Vì \(M\) và \(N\) là trung điểm của \(O A\) và \(O B\), ta có:
- Định lý trung điểm:
- Do \(M\) là trung điểm của \(O A\), và \(N\) là trung điểm của \(O B\), nên các dây \(C D\) và \(E F\) được kẻ song song qua \(M\) và \(N\), do đó các đoạn thẳng này có tính chất đối xứng qua đường nối \(O\) với trung điểm của đoạn \(A B\), tức là \(O\).
- Chứng minh \(O\), \(K\), \(L\) thẳng hàng:
- Vì \(K\) và \(L\) là trung điểm của các đoạn \(C D\) và \(E F\) tương ứng, và do tính chất đối xứng của hình vẽ, các điểm \(O\), \(K\), \(L\) sẽ nằm trên một đường thẳng trung trực của đoạn \(A B\).
Kết luận phần (a): Do đó, \(O\), \(K\), \(L\) thẳng hàng.
Giải phần (b): Chứng minh \(C D F E\) là hình chữ nhật
Cách tiếp cận:
- Đặc điểm các dây song song:
- Dây \(C D\) và \(E F\) là hai dây song song với nhau và cùng nằm trong nửa đường tròn có đường kính \(A B\), tức là \(C\) và \(E\) đều thuộc nửa đường tròn chứa \(A B\).
- Góc vuông tại các điểm \(C\) và \(E\):
- Vì \(C\) và \(E\) nằm trên nửa đường tròn đường kính \(A B\), ta có \(\angle A C B = 90^{\circ}\) và \(\angle A E B = 90^{\circ}\) (theo định lý góc vuông khi có điểm trên đường tròn có đường kính là cạnh huyền).
- Chứng minh hình chữ nhật:
- Các dây \(C D\) và \(E F\) song song và vuông góc với các dây \(A C\) và \(A E\) (do góc vuông tại các điểm \(C\) và \(E\)).
- Các góc tại \(C\), \(D\), \(E\), và \(F\) là góc vuông, và hai cặp cạnh đối diện của tứ giác \(C D F E\) là song song và bằng nhau.
Kết luận phần (b): Do đó, tứ giác \(C D F E\) là hình chữ nhật.
Giải phần (c): Tính diện tích hình chữ nhật \(C D F E\) theo \(R\), khi góc giữa các dây \(C D\) và \(A B\) là 30 độ
Cách tiếp cận:
- Khi góc giữa các dây \(C D\) và \(A B\) là 30 độ:
- Các dây \(C D\) và \(E F\) cùng tạo với đường kính \(A B\) một góc 30 độ. Vì \(C D \parallel E F\), hai dây này đều tạo với \(A B\) một góc 30 độ.
- Ta biết rằng chiều dài của mỗi dây trong hình chữ nhật \(C D F E\) là khoảng cách giữa hai điểm trên đường tròn, và các góc tạo bởi chúng và đường kính \(A B\) ảnh hưởng đến chiều dài các cạnh.
- Tính chiều dài các cạnh của hình chữ nhật:
- Vì góc giữa dây \(C D\) (hay \(E F\)) và đường kính \(A B\) là 30 độ, các cạnh của hình chữ nhật có thể tính bằng công thức liên quan đến bán kính \(R\) và góc.
- Đặc biệt, với góc 30 độ, ta có thể sử dụng công thức:
\(\text{Chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{d} \overset{ˋ}{\text{a}} \text{i}\&\text{nbsp};\text{c}ủ\text{a}\&\text{nbsp};\text{m}ộ\text{t}\&\text{nbsp};\text{c}ạ\text{nh}\&\text{nbsp};\text{c}ủ\text{a}\&\text{nbsp};\text{h} \overset{ˋ}{\imath} \text{nh}\&\text{nbsp};\text{ch}ữ\&\text{nbsp};\text{nh}ậ\text{t} = 2 R sin \left(\right. 30^{\circ} \left.\right) = 2 R \times \frac{1}{2} = R\) - Vậy chiều dài mỗi cạnh của hình chữ nhật là \(R\).
- Tính diện tích hình chữ nhật:
- Diện tích hình chữ nhật \(C D F E\) bằng tích chiều dài và chiều rộng.
- Chiều dài và chiều rộng của hình chữ nhật đều bằng \(R\), do đó diện tích là:
\(\text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch} = R \times R = R^{2}\)
Kết luận phần (c): Diện tích hình chữ nhật \(C D F E\) là
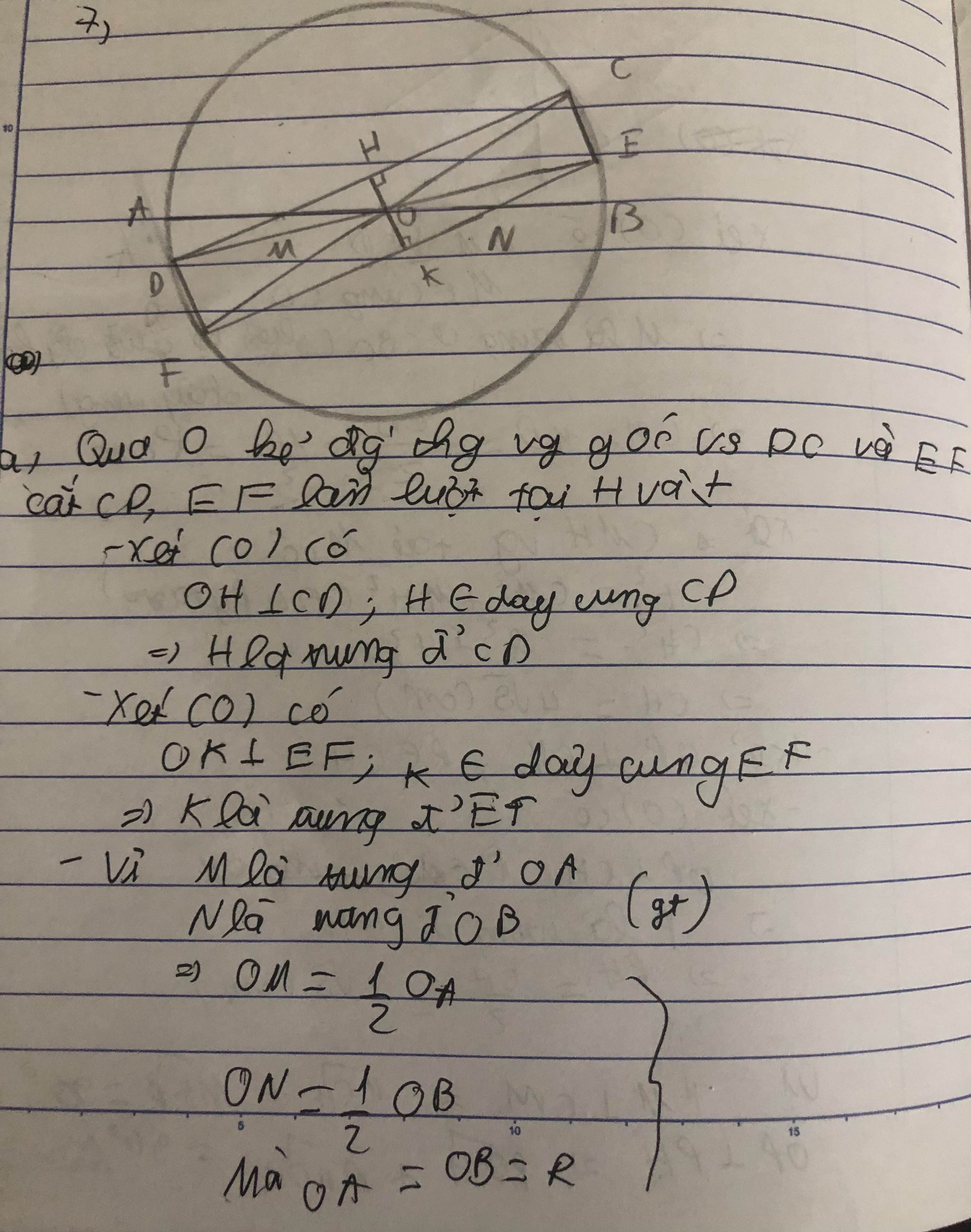
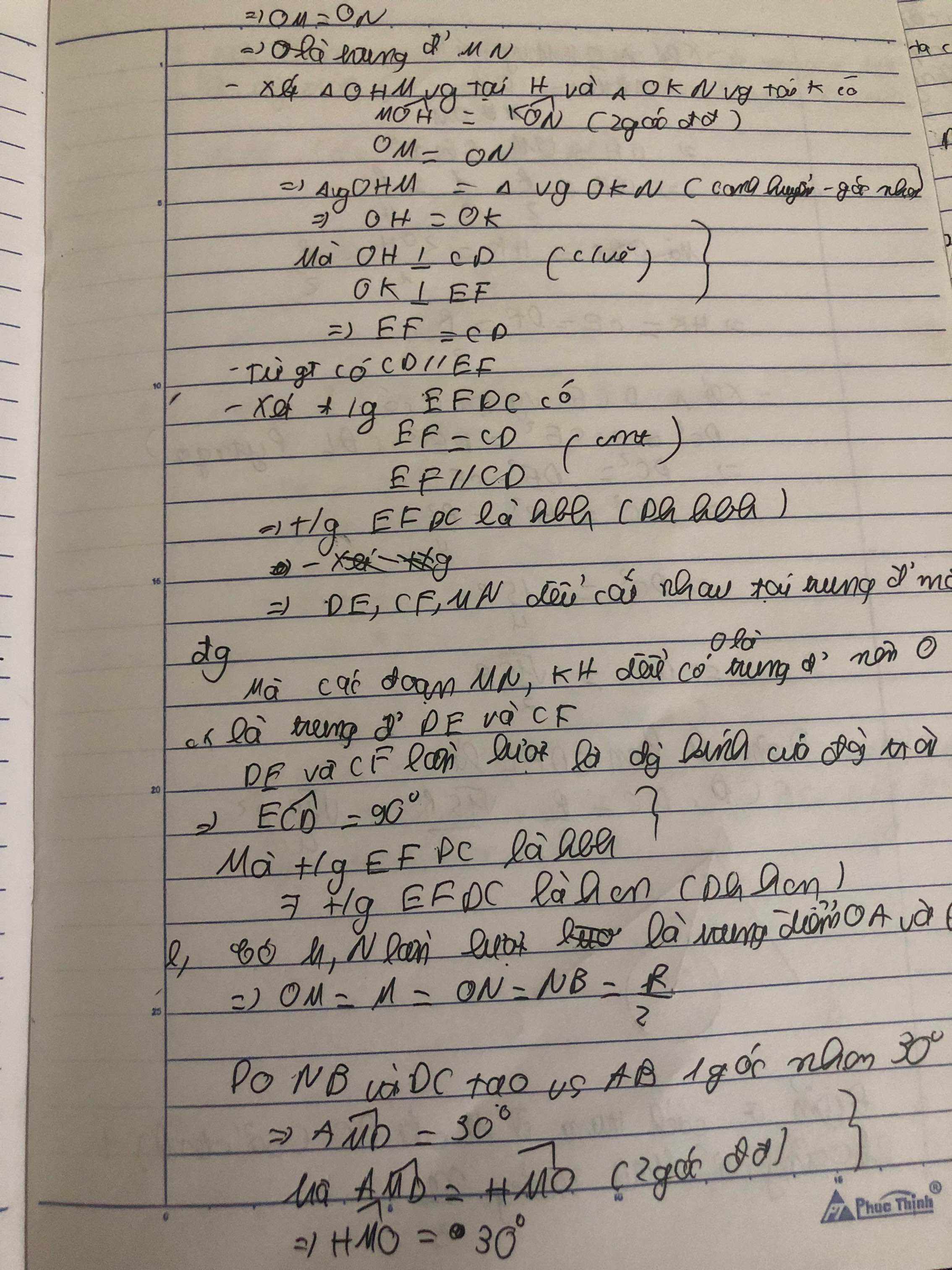

GỌI H,K là chân đường vuông góc kẻ từ O xuống CD và EF.Sau đó chứng minh 3 điểm O,H,Kthẳng hàng.Xét 2 tam giác vuông MOH và NOK bằng nhau.=>CD=EF.=>CDEF là hình bình hành.(1)
Mặt khác ta có OH vuông góc với CD =>CH=MD=1/2CD
OK " " " EF=>KE=KF =1/2EF
=>HK là đường trung bình của hình bình hành CDEF.
=>HK//CE//DF MÀ HK vuông góc với EF =>CE vuông góc với EF.
=>GÓC CEF=90(2)
Từ (1),(2)=>CDEF là hình chữ nhật