Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

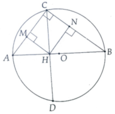
a, Tính được HA=4cm; HB=9cm
b, Tính được HA=4cm; HB=9cm
c, Tính được HM = 12 13 13 cm, HN = 18 13 13 cm
Từ đó tính được S C M H N = 216 13 c m 2

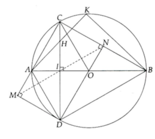
a, HS tự làm
b, Ta có DAHI đồng dạng với DABK (g.g)
=>AH.AK = AI.AB = R 2
c, Chứng minh được I là trung điểm của CD
Từ MCND là hình chữ nhật suy ra MN và CD cắt nhau tại trung điểm của mỗi đường => ĐPCM
d, Chứng minh được I O C ^ = 60 0 => ∆ACO đều nên A C D ^ = 30 0
Chứng minh được DCBD đều nên CD = CB => CD = 25cm
Áp dụng tỉ số lượng giác trong ∆CDM ( M ^ = 90 0 ) ta tính được: MD = 12,5cm và MC = 21,7 cm
Từ đó tính được diện tích xung quanh hình trụ tạo thành khi cho tứ giác MCND quay quanh MD là: S x q = 2 r πh = 542 , 5 πcm 2