Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
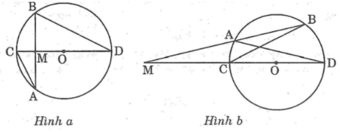
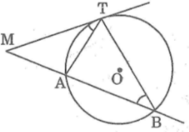
*Trường hợp M nằm bên trong đường tròn (O) (hình a)
Kẻ cát tuyến AB đi qua M và đường thẳng MO cắt đường trong tại C và D
Xét hai tam giác MBD và MCA ta có:
Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (*) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
*Trường hợp M nằm bên ngoài đường tròn (O) (hình b)
Kẻ cát tuyến MAB bất kì của (O) và đường thẳng MO cắt đường tròn tại C và D
Xét hai tam giác MCB và MAD ta có:
Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (**) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
Giải
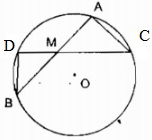
Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D.
Xét hai ∆MAC và ∆MBD:
ˆAMC=ˆBMDAMC^=BMD^ (đối đỉnh)
ˆA=ˆDA^=D^ (hai góc nội tiếp cùng chắn cung BCBC⏜
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
⇒MBMC=MDMA⇒MBMC=MDMA
⇒MA.MB=MC.MD⇒MA.MB=MC.MD (1)
Vì M, O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
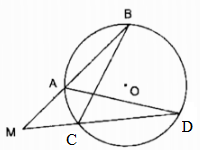
Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
ˆMM^ chung
ˆB=ˆDB^=D^ (hai góc nội tiếp cùng chắn cung ACAC⏜)
Suy ra: ∆MAD đồng dạng ∆MCB (g.g)
⇒MC.MA=MB.MD⇒MA.MB=MC.MD⇒MC.MA=MB.MD⇒MA.MB=MC.MD (3)
Vì M và O cố định suy ra điểm C, D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC. MD không đổi (4)
Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi.
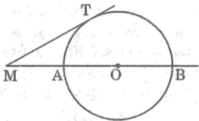
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có M T 2 = MA.MB không phụ thuộc vị trí của cát tuyến MAB.
1) Xét tứ giác MNOP có
\(\widehat{ONM}\) và \(\widehat{OPM}\) là hai góc đối
\(\widehat{ONM}+\widehat{OPM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MNOP là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm của đường tròn ngoại tiếp tứ giác MNOP là trung điểm của OM
hay O' là trung điểm của OM
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi
