Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\widehat{ASC}=\dfrac{sđ\left(\widehat{AB}-\widehat{MC}\right)}{2}\) (1)
(\(\widehat{ASC}\) là góc có đỉnh nằm bên ngoài đường tròn (O)) và \(\widehat{MCA}=\dfrac{sđ\widehat{AM}}{2}\) (2)
(góc nội tiếp chắn cung \(\widehat{AM}\))
Theo giả thiết thì:
AB = AC => \(\widehat{AB}\) = \(\widehat{AC}\) (3)
Từ (1), (2), (3) suy ra:
\(\widehat{AB}-\widehat{MC}=\widehat{AC}-\widehat{MC}=\widehat{AM}\)
Từ đó \(\widehat{ASC}=\widehat{MCA}\).

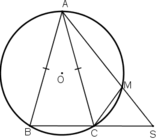
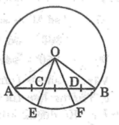
+ Đường tròn (O) có dây AB = AC
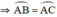
+ 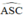 là góc có đỉnh ngoài đường tròn chắn hai cung
là góc có đỉnh ngoài đường tròn chắn hai cung 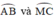

Kiến thức áp dụng
+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

2: góc BEA=1/2*180=90 độ
Xét ΔBMN vuông tại M và ΔBEA vuông tại E có
góc MBN chung
=>ΔBMN đồng dạng với ΔBEA
=>BM/BE=BN/BA
=>BE*BN=BA*BM=BC^2
=>AC^2+BE*BN=AB^2=4*R^2