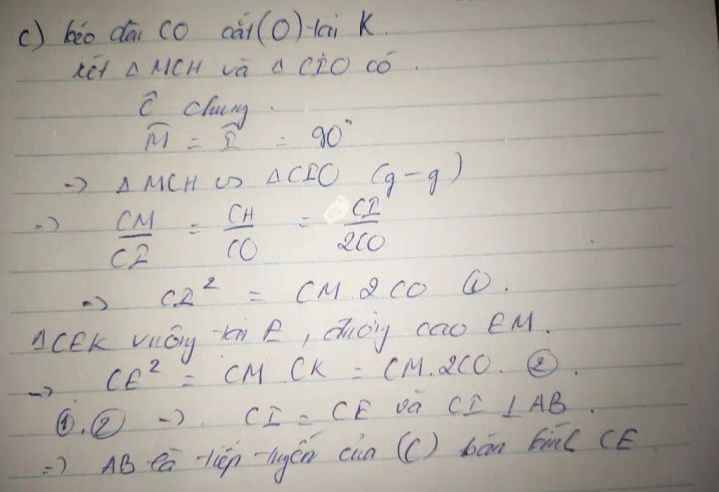Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời hộ mình cái xin. mình đã 2 năm ko on r giờ mới on lại :(((.Xin mọi người trả lời giúp mình :(((

câu 1 sử dụng tính chất góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung là xong nhé
kẻ IK vuông góc với DG và DG cắt đường tròn ngoại tiếp tam giác DFM tại P ==> P là điểm chính giữa cung DF
vì IG vuông góc với DC==> IG // BC
do đó giờ cần chứng minh góc DIG=DBC ( 2 góc đồng vị là ra D;I;B thẳng hàng)
ta có góc DIG=cung DP
góc DMF=1/2cung DF
MÀ cung DP=1/2cung DF( VÌ P là ĐIỂM CHÍNH GIỮA CUNG DF)
==> DIG=DMF
mà góc DMF=DMC( 2 góc nội tiếp cùng chắn 1 cung)
==> góc DIP=DBC
mà DBC+GIB=180 độ==> DIG+GIB=180 độ
==> D;I;B thẳng hàng

a)fac=amo,emo=fca=90 =>efm=emf=>em=ef
b)*dci+dic+idc+ibc+icb+cib=360 mà dci+icb=90;idc+ibc=90 =>dic+cib=180 =>3 diem thang hang
dci+idc+dic=180;cib+icb+ibc=180
*abi=cung ad/2 mà c ko doi =>d ko doi=>ad ko doi=>abi ko doi

A B C M O D
a . i ) Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\Rightarrow CMOA\) nội tiếp đường tròn đường kính CO
Tương tự : = > DMOB nội tiếp
ii ) Vì CM,CA là tiếp tuyến của (O) \(\Rightarrow OC\) là phân giác của \(\widehat{AOM}\)
Tương tự OD là phân giác \(\widehat{BOM}\)
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\Rightarrow OC\perp OD\)
Ta có : CMOA , OBDM nội tiếp
\(\Rightarrow\widehat{AOC}=\widehat{AMC}=\widehat{ABM}=\widehat{OBM}=\widehat{ODM}\) vì CM là tiếp tuyến của (O)
b ) Ta có : \(\widehat{MAB}=60^0\Rightarrow\widehat{DMB}=\widehat{MAB}=60^0\) vì DM là tiếp tuyến của (O)
Mà \(DM=DB\Rightarrow\Delta DMB\) đều
Lại có : \(\widehat{MOB}=2\widehat{MAB}=120^0\)
\(\Rightarrow\frac{S_{MB}}{S_O}=\frac{120^0}{360^0}=\frac{1}{3}\)
\(\Rightarrow S_{MB}=\frac{1}{3}S_O=\frac{1}{3}.\pi.R^2\)