Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trên BC lấy I sao cho IC=IB
Ta có AM=MC=AC/2=20/2= 10 cm
Từ M kẻ MH vuông góc AB. Theo gt, ta được MH=8 cm
Áp dụng Pytago trong tam giác vuông AMH: AH2= AM2 - MH2 = 102 - 82= 36 ----> AH=6 cm
có AM=MC ; IB=IC ---> MI=1/2AB=1/2 .24 =12 cm( đường TB)
Từ I kẻ IK vuông góc AB
có MI// AB( MI là đường trung bình) ; IK//MK (cùng vuông góc AB)
---> MIKH là hình bình hành
---> MI=HK=12 cm; MH=IK=8 cm
BK= AB-AH-HK = 24-6-12=6 cm
Xét tam giác AMH và tam giác BIK:
AH=BK=6
góc AHM= góc BKI= 90O
MH=IK=8
----> tam giác AMH=tam giác BIK(c.g.c)
----> góc MAH= góc IBK (cặp góc tương ứng) hay góc CAB= góc CBA
----> tam giác ABC cân tại C
b) có AM=MC=AC/2=10 cm ; IB=IC= BC/2 ; mà AC=BC (tam giáccân)
----> AM=MC=IB=IC=10 cm
Kéo dài CO cắt AB tại D
tam giác AOC có OA=OC (bán kính) --> tam giác AOC cân tại O
có OM là trung tuyến ---> OM vuông góc AC hay góc OMC=90o
Tương tự với tam giác OCB được OI vuông góc BC hay góc OIC=90o
Xét tam giác vuông OMC và tam giác vuông OIC:
MC=IC=10cm
OC cạnh chung
--->tam giác OMC = tam giác OIC (ch.cgv)
--> góc MCO= góc ICO ---> CO hay CD là phân giác góc ACB của tam giác cân ABC --->
- CD vuông góc AB hay góc ADC=90o
- AD=BD=AB/2 = 12 cm
Theo Pytago trong tam giác ACD: CD2= AC2-AD2 = 202-122 =256 ---> CD=16 cm
Đặt OC=OA=X --> OD= CD-OC = 16 - X
Theo Pytago tam giác AOD: AO2= OD2+AD2
<-->X2= (16-X)2 + 122
<--> 162 -32X + X2 +122 - X2=0
<--> 400 - 32X=0
<--> X= -400/-32= 12,5 cm
Vậy bán kính đường tròn bằng 12,5 cm
tại sao bạn không kẻ đường cao CD. Như thế sẽ đỡ mất thời gian chứng minh
a, Xét tam giác MON có : OM = ON = R
=> tam giác MON cân tại O, do OI vuông MN hay OI là đường cao
đồng thời là đường phân giác => ^MOI = ^ION
Vì BN là tiếp tuyến đường tròn (O) với N là tiếp điểm
=> ON vuông BN hay ^ONB = 900
Xét tam giác IOM và tam giác NOB có :
^IOM = ^NOB ( cmt )
^OIM = ^ONB = 900
Vậy tam giác IOM ~ tam giác NOB ( g.g )
=> \(\frac{IO}{NO}=\frac{IM}{NB}\Rightarrow IO.NB=IM.NO\)
ý b sáng mai mình gửi nhé ;))
sửa hộ mình chỗ này nhé : ^OIM = ^ONB = 900
b, Vì I là trung điểm điểm OA => \(IO=IA=\frac{OA}{2}=\frac{R}{2}\)
Theo định lí Pytago tam giác OIM ta được :
\(MI=\sqrt{OM^2-OI^2}=\sqrt{R^2-\frac{R^2}{4}}=\sqrt{\frac{3R^2}{4}}=\frac{\sqrt{3}R}{2}\)
Vì BM là tiếp tuyến đường tròn (O) và M là tiếp điểm
=> OM vuông MB hay ^OMB = 900 => tam giác OMB vuông tại M
Xét tam giác OMB vuông tại M, đường cao MI
Áp dụng hệ thức : \(\frac{1}{OM^2}+\frac{1}{MB^2}=\frac{1}{MI^2}\Rightarrow\frac{1}{R^2}+\frac{1}{MB^2}=\frac{1}{\frac{3R^2}{4}}\)
\(\Leftrightarrow\frac{1}{R^2}+\frac{1}{MB^2}=\frac{4}{3R^2}\Leftrightarrow\frac{1}{MB^2}=\frac{4}{3R^2}-\frac{1}{R^2}=\frac{1}{3R^2}\Rightarrow MB=\sqrt{3}R\)
CM : tam giác OMB = tam giác ONB ( ch - gn )
Ta có : \(S_{OMNB}=S_{OMB}+S_{ONB}=2S_{OMB}=\frac{2.1}{2}.OM.MB\)
\(=R.\sqrt{3}R=\sqrt{3}R^2\)
Bài 1:
a: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
Suy ra: \(\widehat{ABO}=\widehat{ACO}=90^0\)
hay AC là tiếp tuyến của (O)
b: Xét (O) có
OI là một phần đường kính
CE là dây
OI⊥CE tại I
Do đó: I là trung điểm của CE
Xét ΔDCE có
DI là đường cao
DI là đường trung tuyến
Do đó: ΔDCE cân tại D
Xét ΔOED và ΔOCD có
OE=OC
ED=CD
OD chung
Do đó: ΔOED=ΔOCD
Suy ra: \(\widehat{OED}=\widehat{OCD}=90^0\)
hay DE là tiếp tuyến của (O)
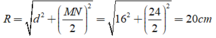
Chọn đáp án D.
Độ dài bán kính của đường tròn là: