Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
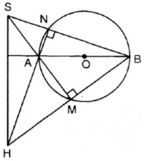
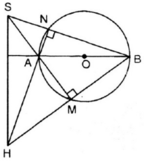
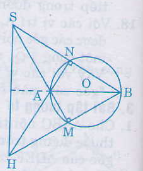
Xét (O) có
^AMB = ^ANB = 900 ( góc nt chắn nửa đường tròn )
nên AN ; BM lần lượt là đường cao
mà AN giao BN = H
=> H là trực tâm => SH là đường cao thứ 3
Vậy SH vuông AB
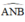là góc nội tiếp chắn nửa đường tròn ⇒ 
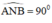⇒ AN ⊥ NB
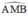là góc nội tiếp chắn nửa đường tròn ⇒ 
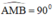⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
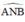là góc nội tiếp chắn nửa đường tròn ⇒ 
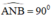⇒ AN ⊥ NB
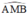là góc nội tiếp chắn nửa đường tròn ⇒ 
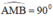⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
BM ⊥ SA ( =
vì là góc nội tiếp chắn nửa đường tròn).
Tương tự, có: AN ⊥ SB
Như vậy BM và AN là hai đường cao của tam giác SAB và H là trực tâm.
Suy ra SH ⊥ AB.
(Trong một tam giác ba đường cao đồng quy)
a:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó;ΔACB vuông tại C
=>BC vuông góc PA
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD vuông góc PB
Xét ΔPAB có
AD,BC là đường cao
AD cắt BC tại Q
Do đó: Q là trực tâm
=>PQ vuông góc AB
mà PH vuông góc AB
nên P,Q,H thẳng hàng
b: Xét tứ giác BHQD có
góc BHQ+góc BDQ=180 độ
=>BHQD nội tiếp
c: Xét tứ giác PCQD có
góc PCQ+góc PDQ=180 độ
=>PCQD nội tiếp
PCQD nội tiếp
=>góc CDQ=góc CPQ=góc APH
HBDQ nội tiếp
=>góc HDQ=góc CBA
mà góc CBA=góc APH(=90 độ-góc PAH)
nên góc CDQ=góc HDQ
=>DQ là phân giác của góc CDH