Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

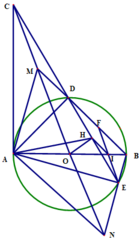
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.

Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F.
Suy ra: Góc HEI = góc HCO
Vì tứ giác AOHC nội tiếp nên:
Góc HAO= góc HEI= góc HCO
<=> Tứ giác AHIE nội tiếp suy ra: góc IHE= góc IAE= góc BDE
=> HI//BD
Mà H là trung điểm của DE
=> I là trung điểm của EF.
Ta có: EF//MN và IE=IF
=> O là trung điểm của đoạn thẳng MN (1)
Từ (1) suy ra:
Tứ giác AMBN là hình bình hành => AM//BN(₫pcm)


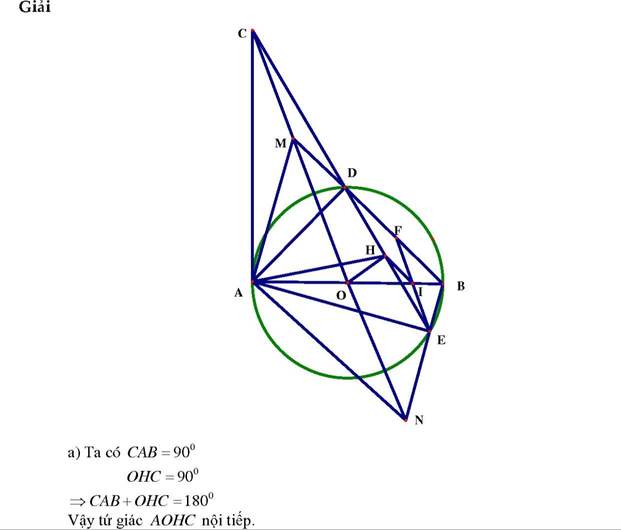
a. Xét tứ giác AOHC có: \(\left\{{}\begin{matrix}\widehat{OAC}=90^0\\\widehat{OHC}=90^0\left(OH\perp DE,C\in tiaED\right)\end{matrix}\right.\)
=> \(\widehat{OAC}=\widehat{OHC}=90^0\)
=> AOHC là tgnt. (tứ giác có tổng 2 góc đối bằng 180 độ)
b. Xét tam giác ACD và tam giác ECA có:
\(\left\{{}\begin{matrix}\widehat{ACD}chung\\\widehat{CAD}=\widehat{CEA}=\dfrac{1}{2}sđ\stackrel\frown{AD}\end{matrix}\right.\)
=> Tg ACD ~ tg ECA (g.g)
=> \(\dfrac{AC}{EC}=\dfrac{AD}{AE}\) => AC.AE=AD.CE