Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
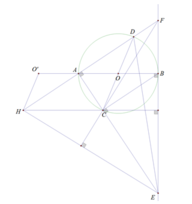
Gọi H là trực tâm tam giác CEF
Ta lại có: C A F ^ = 90 o
3 điểm F, A, H thẳng hàng ⇒ E A H ^ = 90 o
Mà B C E ^ = 90 o
=> A H / / B C A B / / H C
AB = HC = 2R
Gọi O’ làảnh của O qua phép tịnh tiến theo vectơ B A →
OO’ = HC ( = 2R)
MàOO’ // HC ( cùng vuông vớiEF)
O’H = OC = R
Tập hợp H là đường tròn tâm (O’;R)
(CMTT với K là trực tâm tam giác DEF)

- Kẻ đường kính BB’ .Nếu H là trực tâm của tam giác ABC thì AH=B’C. Do C,B’ cố định , cho nên B’C là một véc tơ cố định \(\overrightarrow{\Rightarrow AH}=\overrightarrow{B'C}\)
Theo định nghĩa về phép tịnh tiến điểm A đã biến thành điểm H . Nhưng A lại chạy trên (O;R) cho nên H chạy trên đường tròn (O’;R) là ảnh của (O;R) qua phép tịnh tiến dọc theo \(\overrightarrow{v}=\overrightarrow{B'C}\)
- Cách xác định đường tròn (O’;R) . Từ O kẻ đường thẳng song song với B’C . Sau đó dựng véc tơ : \(\overrightarrow{OO'}=\overrightarrow{B'C}\). Cuối cùng từ O’ quay đường tròn bán kính R từ tâm O’ ta được đường tròn cần tìm .

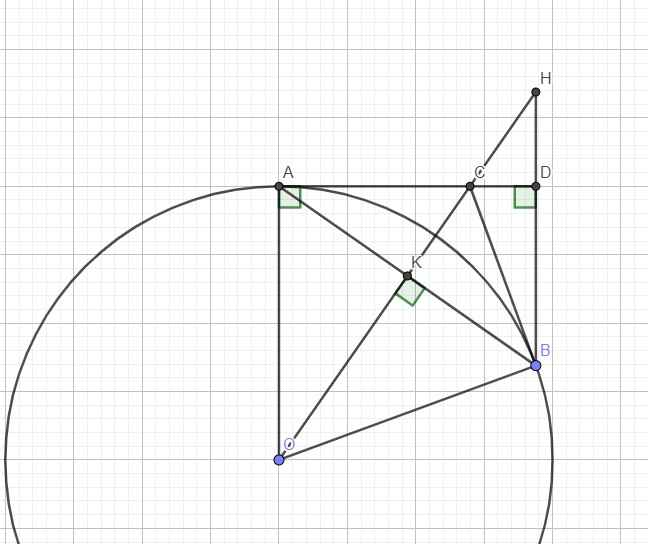
Theo tính chất 2 tiếp tuyến cắt nhau ta có \(AC=BC\)
Mặt khác \(OA=OB=R\)
\(\Rightarrow OC\) là trung trực AB hay \(OC\perp AB\)
\(\Rightarrow\Delta AOK\) vuông tại K
\(\Rightarrow\) Tập hợp K là đường tròn (C) đường kính AO cố định
b.
Do H là trực tâm \(\Rightarrow BH\perp AD\Rightarrow BH||AO\) (cùng vuông góc AD)
\(\Rightarrow\widehat{OAK}=\widehat{KBH}\) (so le trong)
Mà \(AK=BK\) (OC là trung trực AB)
\(\Rightarrow\Delta_VOAK=\Delta_VKBH\left(g.c.g\right)\)
\(\Rightarrow OK=KH\) hay K là trung điểm OH
\(\Rightarrow\overrightarrow{OH}=2\overrightarrow{OK}\Rightarrow H\) là ảnh của K qua phép vị tự tâm O tỉ số \(k=2\)
\(\Rightarrow\) Tập hợp H là đường tròn ảnh của (C) qua phép vị tự tâm O tỉ số \(k=2\) (với (C) là đường tròn đã xác định ở câu a)

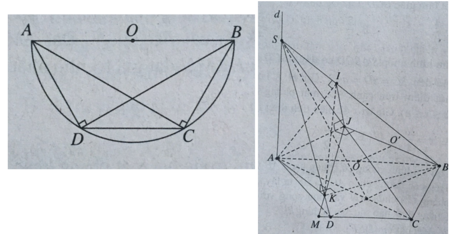
Nhận xét
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).

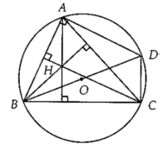
Dễ thấy P là điểm chính giữa \widebatEF\widebatEF nên D,N,P thẳng hàng
Cần chứng minh ˆIMC=ˆPDCIMC^=PDC^
Ta có : ˆIMC=ˆMIB+ˆB1=12ˆBIC+ˆB1=12(180o−ˆB1−ˆC1)+ˆB1IMC^=MIB^+B1^=12BIC^+B1^=12(180o−B1^−C1^)+B1^
=12(180o...



- Tam giác MPQ có QA là một đường cao , vì vậy nếu ta kẻ MM’ vuông góc với PQ thì MM’ cắt QA tại trực tâm H . OA là đường trung bình của tam giác MNH suy ra : \(\overrightarrow{MH}=2\overrightarrow{OA}=\overrightarrow{BA}\). Vậy phép tịnh tiến theo \(\overrightarrow{BA}\) biến điểm M thành điểm H . Nhưng M chạy trên (O;AB) cho nên H chạy trên đường tròn ảnh của (O;AB) qua phép tịnh tiến \(\overrightarrow{BA}\) .
- Tương tự đối với tam giác NPQ .
- Giới hạn quỹ tích . Do M không trùng với A,B cho nên trên đường tròn ảnh bỏ đi hai điểm ảnh của A,B => thỏa mãn yêu cầu bài toán .